1] 数学モデル
非線形運動方程式は古典的形で下記のように表される。
力に対する式は以下のとおり。
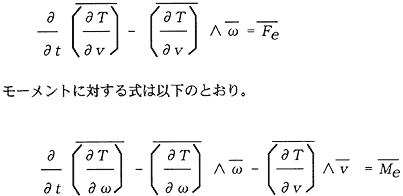
ここに、Tは本体の運動エネルギ、vは速度、ωは角速度、FeとMeは外力とそのモーメントを示す。
完全流体中においては、流体力(付加質量)は本体の運動エネルギを流体Tfの運動エネルギに置き換え、また、速度vを流体と本体の間の相対速度に置き換えるとLamb(1932)の式に完全に一致する。
Tfは速度ポテンシャル関数Φ(x,y,z)を導入することにより下記の式で評価することができる。
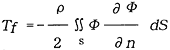
積分は本体表面Sに渡って行なわれ、ηは外向きが普通である。
ポテンシャル関数はHess及びSmith(1967)が提唱した軸対象の流れ又はクロスする流れの中における軸対象物体に対する数値解析により評価された。フィンの効果は相互影響を無視し、Sapkaya及びIsaacson(1981)の準経験則により追加された。
実際の流体を取り扱うときは、粘性力を考慮しなければならない。採用された式はGertler及びHagen(1967)により発展された潜水機に対する標準式を満足している。完全流体の場合と同様に、フィンの効果と主要部の効果は分けて考慮された。フィンによる操縦力はAbott及びVon Doenhoff(1959)により推定された。前進中の抵抗は魚雷型物体に対するGranville(1976)により計算された。抵抗の横方向の力及びモーメントはFeldman(1979)のクロスフロー理論に基づく数値積分により計算された。流れと物体がある角度をなすときの軸対象物体に発生する変動モーメント(正式にはムンクモーメントに一致する)及び揚力はHumphreys及びWatkinsonの式(1985)により考慮された。
6自由度の運動方程式が組み立てられた後、それらはオイラー角の動的関連性に関連する3つの式と共に数値積分することにより解かれた。