1+1が2であることもシミュレーションの入り口であって、現在では多くの方が正しい認識を持たれていると思うが、念のため簡単な事例とともに船舶交通の評価に用いる場合のジレンマにも触れておきたい。
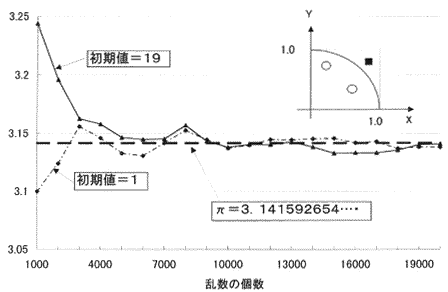
円周率πという不思議な数値は、古来、種々の方法で求められてきたが、ユニークなものとしては地面に描いた円の上に石つぶをばらまき、内外の石つぶの数をかぞえ、その比率から円周率を求める方法がある。無論、まく石つぶが多いほど正確な答えが得られる。
計算機の中でも、より公平で正確にこれと同じことが実行できる。0.0から1.0までの実数を、一様な確率でバラバラに発生させ(乱数)、2つを組にしてX一Y座標値に見立てる。この座標値をグラフ上に落としたとき、円の中に入るか外に出るかをカウントして、円周率を逆算するのである。
用いた乱数の個数により求められる円周率が変動していく様子を図2に試算例として示した。計算機にて発生させる乱数列は、その初期値の与え方によって数値の表われ方が異なるので、図中には2種類の計算結果を示したが、いずれの場合でも、試行を繰り返すにつれて真の値に収束していく様子をご覧いただければと思う。
船舶交通シミュレーションも類似した手法を用いており、確率的な問題を解くのであるから、相応の時間にわたって計算をしなければ普遍性のある答えを導くに至らない訳であり、費やせる時間や経費を勘案しながら、モデルの簡素化と詳細化のはざまでバランスを見出すこととなる。
これまでに提唱された幾つかの船舶交通シミュレーションモデルはそれぞれに特性を持つものであるが、マクロシミュレーションとミクロシミュレーションに大別して利用されているのが現状である。
マクロとミクロは相対比較の問題であり、明確に定義・類別できるものではないが、各船舶の行動を組み込む(モデル化する)程度に相違があると見てよい。これを簡略化すれば、前述した計算処理時間とも絡み、広大な海域にわたって多くの船舶の流れを取り扱える。
図2 乱数によって円周率を求めるシミュレーションの例