where, μB is the constant Value O.8〜0.9,ρ△ is the density difference between ice and sea water, g is the acceleration of gravity, KP is the coefficient of passive stress,HM is the mean channel ice depth, δ is 22.6 degree,μH is the friction coefficient of vessel and ice,φ is the waterline entrance angle at the point of B/4 from the centerline, Ko is the coefficient of lateral stress, LPAR is the length of parallel midbody, AWF is the water line area of foreship, Fn is the Froude number, HF is the term describing the thickness of the brash ice layer. Channel ice is a refrozen broken channel, and it is not used for this simulation.
Ship speed at level ice
The resistance in level ice, RLEVEL is calculated using Lindqvist (Lindqvist,1989) in equation(2.6.4). This resistance consists of three resistant Components: the crushing resistance, the bending resistance, and the resistance of buoyancy force ofice pieccs.
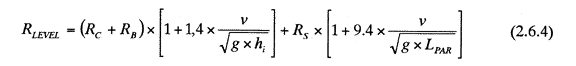
where, RC is the resistance due to crushing, RB is the resistance due to bending, RS is the submergence resistance. On the assumption that RLEVEL is equal to Tnet in the equation(2.6.1), the ship speed was calculated.
Ship speed in ridged ice
As shown in Figure 2.6.2, pressure ridge is modeled with sail height, consolidated layer, and spacing. A ridged ice, as shown in Figure 2.6.2, is modeled as isosceles triangles with two 20 degree angles, where keel depth=5×ridge height, ridge width=27.5×ridge height.
The ridge spacing x is calculated using the following exponential distribution equation(2.6.5):
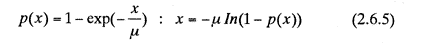
where, p(x):CDF(cumulative distribution function) of ridge space.
μ:mean value of ridge space
The ridge sail height is also expressed using an exponential function of the form: