ここで、D=人間が1日の活動に必要とする熱量(kcal)

10=100tの水が1年間に、1,000kcal人日のエネルギーを生み出すことを示す係数

U=年間更新可能淡水有効水量の利用率(%)

L=生産から消費までの段階で失われる穀物割合(%)

この式は、まず、人間が1日の活動に必要とする熱量(kcal)1年分を生み出す穀物を生産するのに必要な水(X=D kcal/[(1,000　kcal/日/人年)/100t/人年])を求め、ついで、人間の淡水利用率(U)を考慮した必要水量(X/U)を求め、最後に、穀物消失(L)を考慮した必要水量[(X/U)/(1-L)]を求めている。

このようにしてWrが求められれば、これに家庭用の所要淡水量(37m³)⁽¹²⁾を加えて、1人の、人間が1年間に消費する食糧の確保と日常生活のために必要とされる淡水量を計算できる。最後に、水資源からみた最大許容人口(Pmax)は、

Wa=人間が利用しうる更新可能の淡水量とすれば、

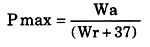
で求められる。

Cohenは、

1]　Uについては、20%(より現実的な水準)⁽¹³⁾と100%(最大可能値だが非現実的水準)

2]　Dについては、2,350kcal(平均摂取熱量)⁽¹⁴⁾と10,000kcal(米国の消費水準)

3]　Lについては、10%(きわめて効率的だが非現実的)と40%(世界の平均的な水準)

4]　Waについては、41,000Km³(世界の有効淡水量)、14,000Km³(現実に利用されている淡水量の推定上限値)、9,000km³(同推定下限値)

の仮定を置いて、各々の組み合わせに基づく最大許容人口を算出している。

その結果、水を最も利用するケース(U=20%、D=10,000kcal、L=40%)では、Waに応じて49億人、17億人、11億人となる。現実の世界人口はこれらを大きく超えていることは言うまでもないが、これは、世界のすべての国が現在の米国並の贅沢な食生活をすることは、水資源の観点からする限りほとんどありえないことを示している。

前ページ　　　目次へ　　　次ページ