フレッチング摩耗は、未だに多くの課題を残している研究途上の問題であるが、これまでに得られた研究成果をもとに、現象の正しい把握と確実な摩耗軽減の方法に焦点を当てて本論をまとめた。紙面の制約もあって、図・表中心の記述となったが、その原稿(Draft)をもとに、講演を行った。本講演の概要は以下の通りである。

[概要]本講演の構成は2部から成り、第1部では、フレッチング摩耗の基礎的諸問題、特に発生メカニズムを考え、第2部では、その防止法を検討した。いずれも筆者とその共同研究者によって過去約20年間に得られた成果を中心にまとめたものである。以下に主要な講演項目と概要を記す。

　

[1]　フレッチング摩耗の発生機構に関する研究

　

[1.1]　MINDLIN理論の検証

　

フレッチング損傷を顕微鏡で直接観察して、従来理論との関連を確かめた結果、球と平面との弾性接触において、静摩擦力よりも小さい接線力が作用するとき、接触面内に存在する固着域とすべり域の割合は、

MINDLINの理論式

a'/a=(1-T/μP)^1/3　　(1)

とほぼ一致することが確かめられた。ただし、a'：固着域(円)の半径、a：すべり域(環)の外半径、T：接線力、μ：静摩擦係数、P：接触荷重である。

　

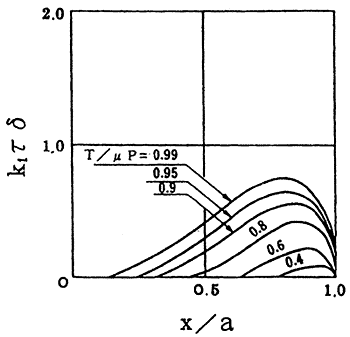
Fig.1 Relation between x/a and τδ.

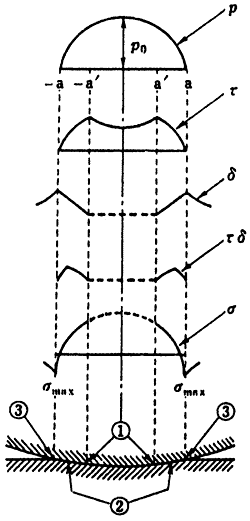
Fig.2 Stress,strain,and other mechanicalparameter profiles for elastic contact between a sphere and a flat plate.

　

[1.2]　フレッチング条件下の応力分布

　

前項に示したように、フレッチング条件下、すなわち、式(1)が成立する範囲では、MINDLIN理論が適用できるから、これに基づいて応力・ひずみ等を求めた結果、τ：接線力Tによる弾性接触面上のせん断応力、δ：Tによる接線方向のひずみ、K₁：定数、x：接触面中心から運動方向にとった距離、a：弾性接触円半径、半サイクルのせん断ひずみエネルギをτδとして、図1が得られる。図示のようにrδは、T/μPの大きさによって異なるが、いずれも最大値がx/a=1以下の場所、すなわち弾性接触円外縁の内側に存在する。また、このときの表面に作用する接線方向の主応力は、弾性接触円の前縁で負(圧縮)、後縁で正(引張)となる。

以上のことをまとめて定性的に示したのが図2である。図中、1、2、3は、摩耗発生の起点位置を意味し、1は最大せん断応力τ_max]による場合、2は最大せん断ひずみエネルギτδ_maxによる場合、3は最大主応力σ_maxによる場合である。

　

[1.3]　ムービーカメラによる直接観察

　

普通のカメラによるフレッチング摩耗の直接観察は、従来、行われていたが、現象が断片的にしかとらえられないために摩耗粉の発生挙動などの観察が十分にできなかった。この点を明らかにするためにムービーカメラによる連続観察記録を行い、現象解明に新しい情報を得ることができた。

それによれば、T＜μPの条件下で生じるフレッチング摩耗は、図2の2の点、すなわちτ δ_maxの位置から始まり、しだいに周囲に広がること、ガラスのようなぜい性材料のフレッチング損傷(亀裂)

前ページ　　　目次へ　　　次ページ