その電流の変化の様子、つまり電荷qの時間的な変化は微分の形で表されdq/dtによって決まる。電荷qは(2.10)式と同様にq=Cvであるから

　

　

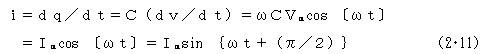
となり、電流iは電圧vに比べ90°(π/2ラジアン)進んでいることになる。こゝで、I_m=ωCV_mである。

このI_m　=ωCV_mをオームの法則のV=IRと比較すると、Rと1/ωCとが対応することになる。このRに対応する量としてXc =1/ωCと置くと、このXc を容量性のリアクタンスと呼び、この値を使うと抵抗と同じような扱いができるようになる。したがって、

Xc =1/ωC=1/2πfC　　　(2・12)

　

である。この容量性リアクタンスの単位は抵抗と同じオームである。この関係から、同じ静電気容量をもったキャパシタに周波数の異なる電源をつないだとき、そのリアクタンスは周波数に比例して小さくなり、そのキャパシタを通る電流値は大きくなることがわかる。

　

図2・7　キャパシタの直列及び並列

　

キャパシタC₁,C₂を図2・7(a)のように直列に接続したときに、このC1とC2に加わる電圧をV₁とV₂とすると、V=V₁+V₂になり、また両キャパシタに蓄えられる電気量Qは同じになるので(2.10)式からQ=C₁V₁=C₂V₂である。したがって、

　

　

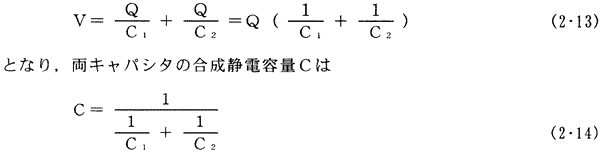
となる。これに対して、両キャパシタC₁,C₂を図2・7(b)に示すように並列接続したときには、Q₁=C₁V、Q₂=C₂V、Q=Q₁+Q₂,Q=CVの関係から

　

C=C₁+C₂　　　(2・15)

　

となり、キャパシタの場合は、抵抗の直列の関係と逆の式となる。

前ページ　　　目次へ　　　次ページ