まず、平衡方程式（1）,（2）式を用いて静水圧型の従動荷重によるシェルの大変形解析を行う。その結果得られた、荷重と変位の関係およびシェルの変形状態をFig. 2に示す。今回の計算例の薄肉シェルでは、従動荷重を増加させていくと飛び移り不安定現象が起こり、この静的に不安定となる荷重を臨界荷重Zmaxと表す。

　次に、運動方程式（4）,（5）式を用いて、静的な従動荷重が負荷されている状態に、さらに擾乱が加わることにより生じる動的挙動について調べる。なお、以降の計算例は静的荷重が臨界荷重Zmaxの80%の載荷状態に対する場合について示す。

　運動方程式の制御パラメータである、擾乱の円振動数ωfと荷重振幅Z'（Z'は荷重振幅Z^*をZmaxで無次元化したもの）からなるωf-Z'平面上における安定領域図を求めた。その結果をFig. 3に示す。この安定領域図は、擾乱により生じるシェルの応答変位の変動幅が擾乱の20000周期の間にシェルの板厚以上となった場合に不安定と判別したものである。ただし、初期条件は（u^*3=0, 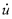^*3=0）としている。また、Fig. 3には固有振動における応答スペクトルを重ねて描いている。ここで、固有振動における応答スペクトルとは、初期値に微小な変位を与え、その応答変位をスペクトル解析したもので、求めたスペクトル図中の応答スペクトルのピークが固有振動数を意味する。Fig. 3より、4種類の固有振動数（A）,（B）,（C）,（D）が存在し、それらの振動数の近傍で安定限界の低下が生じていることが分かる。本研究ではこれらの小さな擾乱により不安定へ移行する領域を対象とする。

　また、固有振動の共振モードを調べることによって、固有振動数ω=（A）138.5,（C）146.3,（B）152.8（rad/sec）近傍は面内振動と曲げ振動の連成振動が支配的な連成共振域、固有振動数ω=（D）241.0（rad/sec）近傍は曲げ振動が支配的な曲げ共振域であることが分かっている。さらに、不安定に至る様相変化の主支配要因が明確な協力現象（Self-organization）型と、多くの要因とその複雑な連成によるセルフ・アセンブル（Self-assembly）型が存在し、協力現象型は曲げ共振域、セルフ・アセンブル型は連成共振域で現れる事が確かめられている。なお、薄肉シェルが動的不安定に至るまでの現象については文献^2）で詳しく述べている。

　

　

　

　

　薄肉シェルの動的挙動は、応答変位の軌道を観察することにより、その安定特性を把握することが有効であり、文献^2）では応答変位の軌道の一断面であるポアンカレ断面の様相変化の定性的な傾向の把握を行った。本研究では、ポアンカレ断面の相関次元を解析することにより、ポアンカレ断面の様相変化を定量化し、応答変位の特性を捉え、動的挙動の把握および安定性判別に利用する。なお、ポアンカレ断面とはカオス挙動の把握のための応答変位軌道における同位相の断面であり、ここでは擾乱の円振動数が2nπ（nは周数で整数）となる断面をとっている。また、相関次元の推定手法は田中ら^5）等で有効性が示されている改良GP法を用いる。

　相関積分を計算することで相関次元を求めるGrassberger-Procaccia（GP）法^8）の一つである、Juddにより提案された改良GP法^6）を用いて相関次元の推定を行う。この方法は、2点間距離の分布を、フラクタル構造を考慮した近似関数^9）で表し、最尤推定法を用いて求めるものである。また、本研究の対象とする運動ではカオス挙動が現れるため、そのアトラクターの幾何学構造がフラクタル構造となっていると予想される。従って、薄肉シェルの動的挙動について相関次元を算出するには、この改良GP法が適していると考えられ、またこの方法を用いることにより、GP法では得られない推定誤差を得ることが出来る。

　改良GP法による相関次元の計算方法は以下の通りである。

　まず、区間BiをBi=［εi+1,εi）, i≥0とする。ただしεi=λⁱε0, λ<1とする。この区間Biに、点Xi（i=1,2,・・・N）の2点間距離が含まれるデータ数biは、次式より求まる。

　

　

　一方、相関次元dを用いて、2点間距離の分布を次式で近似する。

　

　

　これより、区間Bi、に2点間距離が含まれる確率p（bi）は次式となる。

　

　

　ただし、

　次に、用いている未知パラメータ（d,a0,a1・・・at）の推定を最尤推定法で行う。つまり、次式の尤度関数が最大となるように（d,a0,a1・・・at）を決定する。

　

　

　なお、推定範囲はεi≤εcutとして、このεcutをbiが最大となる値から徐々に小さい値まで変化させて調べる。こうして得られる次元dの平均値を推定相関次元D2とし、変動幅を次元の推定誤差hとする。

　実際の計算では数値解析により得られた観測点の時系列データを状態空間に埋め込んで再構成された数値データに対して4.1で説明した相関次元の推定を行う。この場合には、時間遅れ座標系を用いて埋め込みを行っているが、これは時系列データy（t）から（y（t）,y（t+τ）,・・・y（t+（m-1）τ）を構成する方法で、アトラクターの再構成によく用いられている方法である。ここでτは時間遅れ、mは再構成状態空間の次元である。このmを埋め込み次元と呼ぶ。

　埋め込み次元を2, 3, 4, 5と変化させ、それぞれの場合における相関次元の計算を行った。その一例として振動数ωf=242（rad/sec）, 荷重振幅Z'=1.018×10^-3の擾乱の場合について計算した、埋め込み次元と相関次元の関係をFig. 4に示す。これより、m=2では埋め込み次元と相関次元がほぼ等しくなっており、これは再構成状態空間が埋め尽くされている状態であることを意味するので、埋め込み次元が2次元では不十分であることがわかる。また、m≥3で飽和し、埋め込み次元が3次元でほぼ収束していることがわかる。他の擾乱の場合においても、m=2で収束している場合も含め、m=3とすると十分に収束しており、以下の計算例に対しては、3次元の埋め込みで相関次元が推定可能であると考えた。