The deformation and dynamic behavior mechanism of submerged thin shell structures are in principle of a non-conservative nature as circulatory system, because the working load is the follower type as hydrostatic pressure that works vertically to its deformed surface at all times. The disturbance forces of various types, existing in marine environment, lead the complicated dynamic behaviors of the thin shell in the circulatory system of load-deflection. The dynamic behavior of a thin shell undergoing large deflections with small disturbances should be clarified for critical analysis.

 This paper deals with the correlation dimensions corresponding to dynamic behaviors of a thin shell subjected to follower forces with small disturbances. For that purpose, the finite deformation and dynamic behavior of the thin shell are numerically analyzed by the governing equations in a mono-clinically particle coordinates description. Then, the correlation dimensions and Poincare sections are calculated corresponding to dynamic behaviors of a thin shell. By the results of these studies, it is clarified that the correlation dimension related to dynamic behaviors gives an aim of changing from quasi-oscillatory motion to non-periodic motion. Moreover, the correlation dimension makes clear that the difference of the route going to unstable state between two scenarios as "Seif-organization type" instability and "Self-assembly type" instability.

　

　海中の恒温性を利用した余剰食糧の海中貯蔵庫や、有効エネルギー密度が低いために装置が大型化する海水温度差発電所などの海水空間利用を意図して、海中に広く展張する比較的柔軟な海中構造の出現が期待される。そのような海中大空間構造の一つとして、薄肉シェル構造が考えられるが、このような曲率をもつ構造は、従来の耐圧殻とは異なって、水圧による変形のために曲率が変化して曲面のもつ形態抵抗の変化を引き起こし、さらに変形に荷重が追従する非保存系の循環系荷重のために、擾乱による動的挙動は極めて複雑である。このような非保存系の動的挙動は、一般にはカオス挙動^1）となり、動的安定性を判断することが難しい。このため、周期的な運動から非周期運動のカオス挙動への移行、さらに不安定状態に至るまでの動的挙動を把握して、有効な安定性指標を確立することが必要である。

　本研究では、大空間構造の基本的な構造である、水圧型の従動荷重を受ける薄肉シェル構造を対象として、負荷時の擾乱による動的挙動を数値解析し、応答変位、ポアンカレ断面および相関次元の変化の様子を調べる。これにより、薄肉シェルの動的挙動と相関次元の関係を明らかにし、さらに、著者らが文献^2）に示した、不安定に至る様相変化の主支配要因が明確な協力現象（Self-organization）型および多くの要因とその複雑な連成によるセルフ・アセンブル（Self-assembly）型の不安定へ至る過程の違いを明確にする。これらにより、相関次元の安定性指標としての有効性と限界を示し、保存系力学のように固有値判定法が使えない、非保存力学系に対する安定性判別法の確立の基礎とする。

　

　薄肉シェルの大変形および擾乱による運動に関する方程式は文献^2）と同じであるので、ここでは解くべき方程式の概略を説明する。詳細については文献^2）を参照されたい。

　

　従動荷重による薄肉シェルの大変形挙動を表すために、Fig. 1に示すようにシェルの中央面に沿って座標軸（第1,2軸は曲面に接する軸、第3軸はそれらの法線軸よりなる副次2次元座標）をとり、変形に追従する埋め込み一般座標系を用いる。

　

　

　荷重（p¹, p², p³）による大変形の場合の方程式を、含まれる応力テンソルをGreen-Lagrangeひずみテンソルで表し、さらに変位により表すと次式となる。

　

　

　薄肉シェルの動的不安定現象を調べるために、擾乱を脈動荷重と仮定してSmall Vibration Methodを用いる。従動荷重を受けている薄肉シェルが擾乱により振動する場合には、薄肉シェルの変位は、従動荷重による静的な変形量に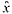（）および擾乱による変動量に（x^*）を添えて表すと、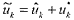となる。

　擾乱による動的挙動を表す方程式は大変形時の平衡方程式（1）,（2）の微小変動分の式に、荷重項を擾乱（曲面の法線方向の脈動荷重）Z^*sinωftに置き換え、さらに慣性項を考慮すると次式となる。ただし、Z^*は擾乱の大きさ（N）であり、ωfは円振動数（rad/sec）である。

　

　

　平衡方程式（1）,（2）式および運動方程式（4）,（5）式を数値的に解くためにGalerkin法を適用して定式化し、載荷時の擾乱による動的挙動はRunge-Kutta-Gill法を用いて数値的に解いて調べる。

　試行する計算例は開き角60°、スパン10mの鋼製（板厚100mm、ヤング率1.96×10¹¹N/m²、ポアソン比0.3、密度7.85×10³kg/m³）の部分球形シェルとし、薄肉シェルの境界条件は面外方向は単純支持、面内方向は変位拘束とする。

　Galerkin法の適用のための近似関数としては次式を用いて数値計算を行う。

　

　

　ここでφk（i,j）（θ¹,θ²）は試行関数であり、境界条件を満たす次式を用いる。ただし、-Ω/2≤θ¹,θ²≤Ω/2（Ωは開き角）である。

　

　

　また、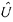k(i,j), U^*k（i,j）は変位の展開係数であり、大たわみ計算では変位増分の係数Δ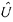k(i,j)および動的挙動の計算ではΔU^*k（i,j）を用いる。なお、変位の展開項数はm, n≥7で荷重−変位の関係は収束した解が得られるが、大たわみ計算では、曲面の変形形状は形態抵抗に直接影響することを考えm=n=9とし、擾乱による動的解析には、擾乱の周波数にもよるが、不安定に繋がり易い低次モードの共振^4）を対象として、計算量を考慮してm=n=3を採った。また、減衰係数に関しては、実際に減衰係数の値を変化させて応答変位を調べ、循環系の現象が現れるC1=C2=0.02およびC3=0.2とした。