|
4.3 クロスフロー抗力
前項の方法により横風圧力係数実験値を使い、クロスフロー抗力係数CCFを決定すると以下のように求まる。
| Fig. 5 |
(a) Calculated cross-flow drag at ψA=90°, CCF, comparing with experimental results and (b) averaged standard errors on CCF for each ship type |
各項の係数の値をTable 3に示す(これより後に得られた係数も同様に示す。)。式中右辺はj=0の定数項を除き、有意なパラメータの順に示す。正面形状と側面形状の特性を表現するパラメータの組み合わせが選択された。C CFの実験値と推定値とを比較しFig. 5(a)に示す。また、次式により船種ごとの平均推定誤差  CF CFを計算し、Fig. 5(b)に示す。
C CFj、 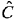 CFj CFjはサンプルjの実験値及び推定値をそれぞれ示す。n Sは対象とする船の数である。 Fig. 5(b)中の「Ave.」は、71隻全船の平均値であり、その値は0.116である。なお、前方法と同様に無次元パラメータのグループ(i)、(ii)、(iii)及びその逆数等の計35パラメータを使って逐次法により求めた推定式の推定誤差と比較した場合、その差は10-3オーダと非常に小さく、少ない数の無次元パラメータから選択した本結果においても適切なパラメータの選択が行われていると考えて良い。
ただし、C CFの実験値は、0.6〜1.3と広範囲に分散した係数となっているが、推定値 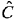 CF CFはそれに比べ狭い範囲のばらつきである。Fig. 5(b)から  CF CFに関してタンカー船型(Tan、Tao、Lng)の推定誤差が大きいことがわかる。1つの要因としては、使用した8船型パラメータのみから個船のデッキ上の形状特性をとらえることが困難であることが考えられる。
| Table 3 |
Coefficients of non-dimensional parameter in the estimating equations |
|
i |
j: 0 |
1 |
2 |
3 |
4 |
| αj |
|
0.404 |
0.368 |
0.902 |
|
|
| βij |
1 |
-0.922 |
0.507 |
1.162 |
|
|
| 2 |
0.018 |
-5.091 |
10.367 |
-3.011 |
-0.341 |
| γij |
1 |
0.116 |
3.345 |
|
|
|
| 2 |
0.446 |
2.192 |
|
|
|
| δij |
1 |
0.458 |
3.245 |
-2.313 |
|
|
| 2 |
-1.901 |
12.727 |
24.407 |
-40.310 |
-5.481 |
| εij |
1 |
-0.585 |
-0.906 |
3.239 |
|
|
| 2 |
-0.314 |
-1.117 |
|
|
|
|
4.4 主流抗力
ψAが0度での主流抗力係数CLF1及び180度での抗力係数CLF2を求めると次式になる。
C LF1とC LF2の無次元パラメータの構成は、前後非対称な船の特徴が反映され、同じとならない。C LF1の実験結果と推定値とを比較しFig. 6(a)に示す。また、平均推定誤差  LF1 LF1を(13)式と同様に計算し、図中(b)に示す。さらにC LF2の場合をFig. 7に示す。全船の平均推定誤差はC LF1の場合0.122、C LF2の場合0.114である。この結果は、C CFの場合と同程度である。 物体の抗力は、高さ、幅、奥行きを組み合わせた比に依存することが知られており23)、前項CCFの場合のHBR/LOA、CLFの場合のAL/LOAB、B/LOA、AF/B2がそれらに相当すると言える。残りのパラメータは、上部構造物の形状の特性を表現している。
| Fig. 6 |
(a) Calculated longitudinal-flow drag at ψA=0°, CLF1, comparing with experimental results and (b) averaged standard errors on CLF1 for each ship type |
| Fig. 7 |
(a) Calculated longitudinal-flow drag at ψA=180°, CLF2, comparing with experimental results and (b) averaged standard errors on CLF2 for each ship type |
4.5 揚力・誘導抗力
初めに揚力・誘導抗力のY方向成分について検討する。0°≤ψ A≤90°及び90°≤ψ A≤180°で場合分けし、(8)式中のC YLIを決定する。クロスフロー抗力の影響が少ないと考えられる風向角の比較的小さい実験値を使用する。C YからF' CFを除き、20°≤ψ A≤40°での平均値を求め、C YLI値とする。船種ごとに平均C YLIを求めFig. 8に示す。横軸には翼理論でのアスペクト比の1/2に相当するA L/ 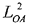 をとる。線形翼理論では揚力係数はアスペクト比に比例増加し、図中一点鎖線で示すπの傾きを持つ直線となる。「Lng」がやや他船と異なる傾向を示すが、本結果においてもC YLIはおよそアスペクト比に対して比例増加している。そこで、次式のようにC YLIを定義する。
右辺第1項は線形揚力項、第2項は船型影響を表す補正項である。逐次法によりCYMを求めると次式になる。
| Fig. 8 |
Averaged lift and induced drag components of lateral force, CYLI, of each ship type |
次に揚力・誘導抗力のx方向成分であるCXLI及び前後抗力補正項のCALFを求める。実験結果から主流抗力成分F'LFを除き、(7)式と実験結果が一致するよう最小自乗法によりCXLI、CALFを決定する。このとき、CXLIはCYLIと同様にアスペクト比に対して比例増加する係数であるが、傾向がCYLIの場合と異なるため逐次法により直接CXLIを求めることにする。解析を行い、得られた結果を次式に示す。
さらにCALFを次式に示す。
なお、主としてCXLIに関してψA=90°は不連続な風向角になるが、前後非対称性の影響を含め、値を0とせずψA=80°からψA=100°で滑らかに接合させる。
0°≤ψ A≤90°のy方向揚力・誘導抗力成分C YLIの最大値を実験値と推定値で比較しFig. 9(a)に示す。さらに次式により平均推定誤差  YLI YLIを定義し、船種ごとにFig. 9(b)に示す。
ここでC YLIjkはサンプルjの揚力・誘導抗力成分実験値、同様に 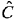 YLIjk YLIjkは計算により求められた値、n ψは風向角数19である。また、Fig. 9(b)に全船の誤差平均を「Ave.」として示す。Fig. 4からもわかるようにC CFに比べC YLIは小さい値であることから全船誤差平均も0.074と小さな値となっている。「Lng」に関しては、Fig. 8で示されたように他船とは異なる傾向であったことから、推定誤差が大きくなっている。 以上、(7)式、(8)式を構成するために必要な係数を8の船体外観形状パラメータを使って表現することができた。
| Fig. 9 |
(a) Averaged maximum values of lift and induced drag components on calculated lateral force, CYLI, at 0°≤ψA≤90° comparing with experimental results and (b) averaged standard errors on CYLI for each ship type |
|