次に観測Otを考慮し、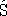tからStを求める。具体的には、各標本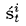ごとにOtの尤度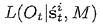に従って重みωⁱを決定し、こうして得られる標本と重みの集合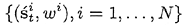から重みに比例する割合でN点の無作為抽出を行う。重みが大きい標本ほど「ありうる」標本であるから、こうして抽出されたStはp（xt|xt-1, at-1, Ot, M）を表現するものと考えられる。

　これ以降標本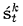について考えるものとし、添え字k, tは省略する。観測Oがn点の観測点o¹，o²,..., oⁿからなる場合、それぞれの観測点は独立事象であるため

　

　

とする。Fig. 3のように観測点Oⁱから最も近い線分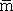までの距離をdとすると、センサの計測誤差は平均値がゼロのガウス分布に従うと考えられるから、観測点Oⁱの尤度は密度関数

　

　

を用いて

　

　

と計算される。

　しかしながら、水中環境においては水中の浮遊物を計測したり、ソーナーの場合はマルチパスによるノイズを拾ったり、シートレーザの場合は画像処理の失敗などによって、ガウス分布では説明のつかない誤差を生じることがある。また、ソーナーの場合入射角が大きいと計測値が信用できなくなる。そこでこのようなエラーを適切に評価するためにエラー定数eを導入し、以下の二つの条件をクリアできた場合に限り（10）式を適用する。

　

　

　

　上記の条件が一つでも満たされなかった場合、

　

　

とする。なお、σはセンサの計測誤差σsと環境マップの不確実性σmから以下の式により求める。

　

　

　本手法はロボットの状態xがマップ上でリアルタイムに推定されることを前提として、観測経路Wに沿って航行するための制御目標値Rを与える。制御目標値を実現するためのローレベルコントローラについては議論しない。

　まず行動を開始する前に自己位置をある程度の精度で求めておく必要がある。そこで自己位置の標準偏差σrが閾値σmaxより大きい場合、位置保持しながら自己位置が収束するのを待つ。自己位置が確定したら、次に進路がクリアかどうかを確認する。このためには、Fig. 4に示した自己位置rから目標航路点wiまでのベクトル

　

　

がマップMと交差しないことが条件となる。

　水平位置に関しては航路点wiに対する方位制御を行うものとし、深度目標zrefはwiの深度とする。即ち制御目標値R={uref, ωref, zref｝は目標航路点までの直線距離|t|、方位偏差dψ、目標航路点の深度ziを用いて以下の式により決定する。

　

　

　但しg（x, a, b）は比例係数aと値域bを持つ比例関数

　

　

であり、方位偏差dψが閾値より大きければuref=0とする。

　航路点の到達条件は|t|＜ωrとし、全ての航路点を通過した時点でミッション終了となる。