|
4. 結言
本論文では、固定ピッチプロペラ型風力発電機の発電効率を改善する一つの方法として、ロータの最適回転数制御に関する研究を行った。はじめに、数学モデルが風速変動に強い影響を受けることに着目し、各運転モードに対してスケジューリング制御の一つであるLPV制御系設計を行った。次に、そのコントローラの性能を検証するために、数値シミュレーションを行ったところ、いづれの運転モードにおいてもLPV制御は従来制御よりも十分な制御性能を確認することができた。今後は、実験を通してその性能を評価すること、また、本論文で適用した制御手法を、洋上で扱われるような大型風力発電機へ適用することが課題である。
参考文献
1)牛山 泉: 風車工学入門 −基礎理論から風力発電技術まで−, 森北出版株式会社, 2002.
2)加藤和彦: NEDOにおける風力発電技術の開発現状と課題, 風力エネルギー利用シンポジウム, 2002.
3)涌井徹也, 橋詰匠, 斉藤久男, 長尾利夫: 自立電源用風力発電システムの変速制御運転に関する研究, 風力エネルギー利用シンポジウム, 2002.
4)大屋祐二, 鳥谷隆, 桜井晃, 井上雅弘: 風レンズ効果(風エネルギーの集中)による風力発電の高出力化, 風力エネルギー利用シンポジウム, 2001.
5)R. Datta and V.T. Ranganathan: A Method of Tracking the Peak Power Points for a Variable Speed Wind Energy Conversion System, IEEE Trans. Energy Conv.,, no.1, vol.18, 2003, pp 163-168.
6)W. E. Leithead, D. J. Leith, F. Hardan and H. Markou: Global Gain-scheduling Control for Variable Speed Wind Turbines, Proceedings of European Wind Energy Conference EWEC '99, 1999.
7)H. D. Battista, R. J. Mantz and C. F. Christiansen: Energy-based approach to the output feedback control of wind energy systems, Int. J. Control, no.3, vol.76, 2003, pp 299-308.
8)p. Apkarian, G. Becker, p. Gahinet and H. Kajiwara: LMI Techniques in Control Engineering from Theory to Practice , Workshop Notes CDC,, Kobe, Japan, Dec, 1996.
付録
ここでは、(23)式の証明として、2つのスケジューリングパラメータを持つ場合のシステム表現について説明する。Fig. 12に示すような三角形領域を考える。
| Fig. 12 |
Description of the LPV system using two scheduling parameters |
線分 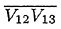 上の点V(x, y)は、
と表すことが出来る。また、α≠0と仮定すると、
となる。さらに、点Vが線分 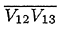 をβ:(1-β)に内分するものとすると、
という関係が満足される。ただし、
である。(29)式を整理すると
となる。仮定を満足しないα=0の場合について考えると、(30)式から[x, y]T=[x1, y1]Tとなっており、正しく表現されることが分かる。
ゆえに、2つのスケジューリングパラメータを持つシステムは、1つの平面内で変動するために、上述したシステム表現により、線形補間タイプのLPVシステムに変換することができる。
|