交流回路では一般に電圧、e、電流、i、のように小文字で表現する。電圧、eを抵抗に加えたときの電流、i、は電圧の変化と一致（同位相）するが、コイルに流れる、電流iLは電圧より遅れた位相で変化し、コンデンサに流れる電流、iCは逆に進む位相変化をする。

　図1・11にこれらの電圧と電流波形の位相関係を示す。

　コイルとコンデンサの交流におけるリアクタンス（等価抵抗）XLとXCは電流の大きさを変えると共に、加える電圧eの変化に対して図1・11に示すようにコイルの電流iLは遅れ、コンデンサの電流iCは進む位相で変化する。

　次に示すようにコンデンサは電極間に帯電した電気量を充電と放電を行い、コイルは流す電流により磁界が発生する現象があるため加えた電圧に対して流れる電流がコンデンサでは進み、コイルでは遅れて変化する。これらを、位相が進む、及び、位相が遅れる、と呼ぶ。

　

　

コンデンサ：

　図1・12に示すような2枚の導体板を並行に近づけて置いた電気素子をコンデンサと呼ぶ。コンデンサに電圧を加えると導体板（電極という）の間に電気量がたまる。コンデンサに直流電圧を加えると電極間に電気量がたまるまで充電電流が流れるが電気量が一杯に蓄電されるとコンデンサに電流が流れなくなる。図1・12（左）は充電する状態を示す。充電されたコンデンサの電極間を（右）図のように導線で結ぶと蓄電された電気量が放電電流となって反対向きに流れ出る。コンデンサは電気量を蓄えるだけで放電が終わると電流が流れ出なくなる。

　電池は化学作用で電気量を造り出すことができるので電池の寿命が終わるまで電流を連続して取り出すことができるがコンデンサは放電が終わると電流が流れなくなる。このためコンデンサは直流を阻止する役目に使用される。コンデンサに交流又は高周波を加えると、プラスとマイナスの極性が反転するたびにコンデンサが充電と放電を交互に繰り返すことからコンデンサを通して電流が流れる。コンデンサは直流を阻止するが交流や高周波を通す役目をする。

　

　

　

　コンデンサに電気を蓄える能力を静電容量又は単に容量と呼び、容量の単位に（ファラッドF）が用いられる。1Fの単位が大き過ぎるので通常は10⁶分の1の1マイクロファラド（μF）又は10¹²分の1の1ピコファラド（pF）が用いられている。コンデンサの記号にCが用いられる。

　コンデンサは次に説明するコイルと組合せて特定の周波数を選択する共振回路としても利用される。

　コンデンサに交流電流iCを流すと抵抗と同じに電流を阻止する性質があり、これをコンデンサのリアクタンスXCと呼び、オームの法則と同様に

の関係がある。コンデンサのリアクタンスXCは

　

　

となる。コンデンサに流れる電流iCは（1・12）式、（1・13）式から

となる。ここで、fは周波数、Cは静電容量、jは虚数単位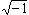である。（1・14）式の右辺にjがあることは電流iCが電圧eの変化より位相角で90度進んで変化しながら流れることを示している。

　抵抗に対するオームの法則（1・5）式はjがないので、抵抗に交流電圧を加えるときの電流の変化は電圧と同じ波形（同位相）で流れる。

コイル：

　図1・13（a）に示したような導線をら線形状に巻いた素子をコイルと呼ぶ。コイルに電流を流すとアンペアの法則に従って磁力線が発生する。磁力線については次の1・2 項で説明する。磁力線は電気力線と同様な磁気の力を作用させる仮想上の線である。

　コイルに電流を流すと磁力線が発生して抵抗と同じ作用をするコイルのリアクタンスXLを発生する。

　

　

　

　

　コイルに加える電圧e、流れる電流iLとの間にはリアクタンスXLを用いて

の関係がある。ここでXLは

となり、Lはコイルの定数（インダクタンス）で、巻き回数、直径、導線の太さなどで定まり、単位はヘンリーで表す。jは虚数単位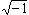で、電圧eを加えたとき流れる電流iLは

　

　

となる。（1・17）式右辺の-jは交流電圧の変化に対して電流の変化が位相角で90度遅れることを示す。インダクタンスLが大きいほど抵抗作用が大きくなるのでコイルに流れる電流iLが小さくなる。

　コイルとコンデンサを組合せると固有の周波数を選択することができる。1・1・6項でこの共振回路を説明する。

　図1・14にコイルとコンデンサ回路を記号で示す。