|
8・2・7 電灯の効率
ある光源の発する全光束とそれの入力との比を電灯の効率という。
電灯効率 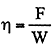 η=F/W F:全光束〔 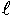 m〕 W:電灯の入力〔W〕
作業面(特記ない場合は床上85〔cm〕で室の全体にわたる水平面)に投ずる光束と設備された電球全体が発する光束との比をいう。またこれを利用率ともいう。記号としてはUを用いる。
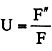 F:電球全部の光束 F":作業面に投ずる光束
照明器具から発散される光束と器具内におさめられた電球の全光束との比を器具効率という。記号としてkを用いる。
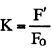 F':器具から発散される光束 F o:電球の全光束 (法線照度という)
I:光度〔cd〕、 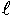 :光源からの距離〔m〕 これを距離の逆二乗法則という。
I:光度〔cd〕、θ:光源の入射角、 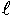 :距離〔m〕 これを入射角の余弦法則という。
〔例題〕1. 8・3・2における図において入射角θが30°であるとき光度が120〔cd〕の均等点光源からの2〔m〕の距離にあるP点の照度はいくらか。
〔解〕 8・3・2における式から
〔例題〕2. I〔cd〕の点火源からr〔m〕離れた球の内面照度 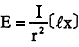 であることを証明せよ。 〔解〕 点光源から放射する光束は一様であるから球内面上の入射光束密度も一様である。
また球の内面積=4πr 2〔m 2〕、一点光源からの立体角ω=4π〔sr〕、点光源からの全光束F=4πI〔 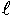 m〕である。 ある点光源からある面上の照度はその面のあり方によって違ってくる。通常法線照度、水平面照度、鉛直面照度の三つの場合について考える。下記の図はこれらの関係を示す。
Ev 鉛直面とφの角をなす鉛直面
照度:Evφとする。
以上の関係式から面上の点Pにおける照度は次式による。ここでI:点光源の光度〔cd〕とする。(8・3・1参照のこと)
また 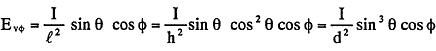 注:大きさのある光源の最大寸法が距離 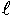 の約1/10以下であれば点光源とみなしてさしつかえない。 〔例題〕
上図において床面BCからの高さ3〔m〕、壁ABからの距離4〔m〕の所にある光源L〔cd〕によって隅B点の床上に生ずる照度を20〔 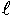 x〕とすればBに向かう方向の光度はいくらか。またBにおける壁面の照度はいくらか。 〔解〕 床上に生ずる照度が水平面照度、壁面の照度が鉛直面照度であるから、床上に生ずる照度Ehについては8・4の(2)式から、また光源LからBに向かう方向の光度をIとすれば、
上図において、球O光源からP点の照度を求める。P点から球に接する円錐APBを考えればABを直径とする平円板光源と同様である。
P点照度 E=πBsin 2θ=I/X 2〔 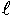 x〕 B':光源の輝度〔sb〕=〔cd/cm2〕
(cm単位で計算の場合使用)
B:B'×104〔cd/m2〕
(メートル単位で計算の場合使用)
I:球光源の光度=πBr2〔cd〕
〔例題〕
上図において直径D〔m〕の半球形乳白色ガラスの照明器具の頂面は床面上からH〔m〕の高さである。ガラス球の輝度はB〔sb〕とし器具の中心から直下の床上P点の水平面照度はいくらか。
ただし天井及び壁の反射は無視し、かつ直径Dは高さHに比較しある程度大きいものとする。
〔解〕8・5の式 E=πBsin 2θ〔  x〕であるから B=B'×104、sinθ=(D/2)/Hを代入すれば
|