|
6・3 三相誘導電動機
P 1= 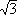 VI cosθ〔W〕 V:供給電圧〔V〕、I:線電流〔A〕、cosθ:力率(小数)
η:効率(小数)
注:通常電動機は出力〔W〕で表しているから、電力調査表の入力の計算にはPo/ηで計算すること。
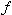 :周波数〔Hz〕、P:全極数
N:回転数毎分(定格負荷時)、n:回転数毎秒(定格負荷時)
P0:ワットで表した電動機出力、cosθ1:一次(固定子)力率(小数)
V 1I 1:入力〔VA〕、η a= 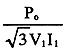 ・・・皮相効率(小数)
(1)同期ワット
P2:二次側(回転子)入力〔W〕、ns:同期速度〔s-1〕
このP2は同期速度で回転した場合に発生すると考えられる機械動力で、これを同期ワットといい、トルクをいい表す一つの方法である。
〔例題〕4極、60〔Hz〕の三相誘導電動機がトルク9.74〔kg・m〕を発生し、速度1,750〔min-1〕で回転するとき、同期ワットで表したトルクを求めよ。
〔解〕 T=9.8×9.74=95.5〔N・m〕・・・kg・mをN・mに変換
それ故 P2=T×2πns=95.5×2π×30=18,001〔W〕
(2)トルク
上記(1)式は(2)式にて表すこともできる。
E2:誘導電動機の回転子電圧〔V〕
s:すべり(小数)
r2:回転子回路の抵抗〔Ω〕
x 2:回転子回路のもれリアクタンス〔Ω〕=2π 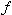 L k2:定数
この式から誘導電動機のトルク〔T〕は電圧の自乗に比例することがわかる。
(3)停動トルク(最大トルク)
この条件は、E2を一定として、s=r2/x2なる条件を(2)の式に入れたものである。実際にはE2が変わるので大約を示したものである。実状ではTmに相当するすべり(s)の値は13〜30%である。
(4)始動トルク
(2)式において、s=1とおけばよい。
(5)トルクの比例推移
最大トルクは誘導電動機の固有のものであるが、移動ができる。
次のトルク式
からわかるように(r2/s)の関数であるから、r2をm倍すれば、トルクは前のすべりsのm倍の点で発生する(上図参照のこと)。
したがって始動トルクを最大にするためにはすなわち最大トルクがs=1のときに発生するようにr2の値を定めることにある。この性質をトルクの比例推移という。巻線形誘導電動機に応用される。
〔例題〕1. 6極で60〔Hz〕の巻線形誘導電動機がある。全負荷速度は1,152〔min-1〕、二次一相の抵抗は2〔Ω〕とし、速度を960〔min-1〕にするために挿入する外部抵抗rを求めよ。
〔解〕
よって上記(4)式から
〔例題〕2. 上記の問題で負荷抵抗8〔Ω〕を二次一相に入れた状態で、始動時に最大トルク〔Tm〕を発生するための電動機二次一相のもれリアクタンスは何〔Ω〕あればよいか。
〔解〕 上記(3)式を満足するためには
始動時には s=1であるから
V1、V2:電動機の始動電圧(相電圧)〔V〕
Ts1、Ts2、:V1、V2に対する始動トルク
(1)Y−△始動方式
Is1:Y結線 Id2:△結線に変更
(2)始動補償器による始動方式
Ic1:始動補償器による始動電流
Ic2:全電圧始動時による電源電流
a:単巻変圧器の変圧比
t1:負荷時分〔m〕、t2:無負荷時分〔m〕
注:通常はt1+t2を1周期とし10min以下とする。そして15、25、40%が標準である。
|