|
1・2 静電気・電流による磁界
C:静電容量ファラド〔F〕、Q:電荷クーロン〔C〕、V:電位ボルト〔V〕
(注)ファラド〔F〕は実用上大きいので1〔μF〕=10-6〔F〕、1pF=10-12〔F〕が用いられる。
S:板の面積〔m2〕、t:板間の距離〔m〕、εs:板間の媒質の比誘導率
比誘導率εsの例
エボナイト 2.8
マイカ 2.5〜2.6
紙 2.0〜2.6
陶器 5.7〜6.8
ゴム 2.0〜3.5
〔例題〕板電極の面積Sが100〔cm2〕で、間隔tが2〔mm〕両極間の媒質の比誘電率εsが2であるときの、両極間の静電容量〔C〕はいくらか。
(1)直列接続
(2)並列接続
C=C1+C2+C3+・・・〔F〕
〔例題〕2〔μF〕、3〔μF〕、4〔μF〕の3個のコンデンサを直列に接続した場合と、並列に接続した場合についてそれぞれ合成静電容量を求めよ。
〔解〕 直列の場合  並列の場合 C=C1+C2+C3=2+3+4=9〔μF〕
H=  〔A/m〕又は〔AT/m〕 H:磁界の強さ〔A/m〕又は〔AT/m〕、
r:考える点までの距離〔m〕
I:電流〔A〕
H=  〔A/m〕 N:全巻数、r:半径〔m〕
(実際には無限長ソレノイドはないが、断面に比べて長さが長いならば近似的に次に示す磁界となる)
N=NoI〔A/m〕
No=単位長1〔m〕あたりの巻数
U=IN〔A〕又は〔AT〕
U:起磁力アンペア〔A〕又はアンペア回数〔AT〕、I:電流アンペア〔A〕
N:コイルの巻数
H:単位長あたりの起磁力〔A/m〕又は〔AT/m〕、 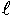 :磁路の長さ〔m〕
φ:磁化された鉄心中の全磁束ウェーバ〔Wb〕、B:磁束密度毎平方メートル〔Wb/m2〕、S:鉄心の断面積〔m2〕、R:磁気抵抗〔A/Wb〕
次の関係があるR=  、 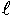 :磁路の長さ〔m〕、μ=μ sμ oμs:比透磁率真空では1、空気中では約1、μo:真空の透磁率、
μo=4π×10-7〔Wb/Am〕又は〔H/m〕
〔例題〕
上図における鉄心入りの磁気回路の
(1)起磁力U (2)磁気抵抗R
(3)磁束φ (4)磁束密度B
をそれぞれ求めよ。
〔解〕
(注)計算途中でπ=3.1416などのような定数は3.14として計算しないで、計算の最後までπとして残し、その後、3.14に置きかえ計算する方が計算しやすいことに注意すること、なお、交流回路計算においても、 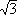 などもこれに類する。 |