|
1・1・7 オームの法則
上図の電気回路で次の関係がある。
〔例題〕1. 電気アイロンを100〔V〕の電灯線に接続したら、2.5〔A〕の電流が流れたという。
この電気アイロンの抵抗は何〔Ω〕か。
〔解〕
〔例題〕2. 抵抗Rが20〔Ω〕の導体に5〔A〕の直流が流れているとき、この導体の両端間の電位差は何〔V〕か。
〔解〕 V=RI=20×5=100〔V〕
〔例題〕3. 抵抗Rが20〔Ω〕の電気回路の両端に200〔V〕の直流電圧を加えたとき、回路に流れる電流は何〔A〕か。
〔解〕
R:電気抵抗〔Ω〕、ρ:抵抗率(体積固有抵抗)〔Ω・m〕、 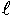 :導体の長さ〔m〕 s:導体の断面積〔m2〕
R':電線の抵抗、ρ':抵抗率(固有抵抗)〔Ω/m/mm2〕、軟銅1/58、硬銅1/55、
アルミニウム線1/35、s':電線断面積〔mm 2〕、 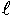 :電線の長さ〔m〕 G:コンダクタンス モー〔 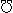 〕又はジーメンス〔s〕、 1/ρ=σ導電率〔 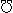 /m〕又はジーメンス毎メートル〔s/m〕 〔例題〕直径が2〔mm〕で長さが500〔m〕の銅線の抵抗〔R〕は何〔Ω〕か。
ただし鋼線の抵抗率ρ'は1/58〔Ω/m/mm2〕とする。
〔解〕
ただしrは銅線の半径
RT=Ro(1+αoT)〔Ω〕・・・(1)(一般の場合)
RT=Rt{1+αt(T-t)}〔Ω〕・・・(2)(一般の場合)
RT、Ro、Rt:それぞれ温度T、O、t〔℃〕における抵抗〔Ω〕
αo、αt:それぞれ温度O、t〔℃〕における抵抗の温度係数〔Ω/℃〕
よって(2)式
〔例題〕温度20〔℃〕のとき、抵抗が10〔Ω〕の銅線が、100〔℃〕のときの抵抗R 100は何〔Ω〕か。ただし 軟銅の抵抗の温度係数を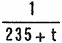 とする。 とする。〔解〕
θ:温度上昇〔℃〕、T:熱状態の最終温度〔℃〕、
t:冷状態の当初の温度〔℃〕、RT:T〔℃〕における抵抗〔Ω〕
Rt:t〔℃〕における抵抗〔Ω〕
αt:t〔℃〕における抵抗の温度係数〔Ω/℃〕
θ':熱状態での温度上昇〔℃〕、t2:熱状態の銅線温度〔℃〕
ta:温度試験の最初の基準周囲温度〔℃〕、t1:冷状態の銅線温度〔℃〕
R1:冷状態の銅線抵抗(当初の抵抗)〔Ω〕
R2:熱状態の銅線抵抗(最終抵抗)〔Ω〕
〔例題〕運転開始前の発電機の巻線の抵抗を測定したら、周囲温度20〔℃〕の時0.25〔Ω〕であった。次に運転を開始し、しばらくの後停止し、直ちに抵抗測定したら0.295〔Ω〕であった。巻線の温度はいくらになったか、また巻線の温度上昇はいくらか。
ただし銅線の20〔℃〕における抵抗の温度係数= 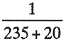 とする。 〔解〕 ta=20〔℃〕、R2=0.295〔Ω〕、R1=0.25〔Ω〕、t1=ta=20℃とする。
巻線の温度=20+45.9=65.9〔℃〕
巻線の温度上昇=45.9〔℃〕
|