6.1 Wind Tunnel Test for Upwind

　

 In order to investigate the tacking maneuver of this ship, we performed the simulation study. For the simulation, we need the aerodynamic coefficients of sail in upwind condition. Because the coefficients indicated in Figure 9 are not sufficient to evaluate the performance in upwind condition, we carried out the wind tunnel test again and the numerical calculation. The wind tunnel test was performed at the Kyushu University Wind Tunnel with circular measurement section of 2.0m in diameter. Wind velocity was 7m/s, which was same condition with the experiment in the reference [1]. The comparison of results between the wind tunnel test and the numerical calculation is mentioned in the section 6.3.

　

6.2 Sail Force Calculation by Vortex Lattice Method

　

 Aerodynamic forces acting on the sail in upwind condition are calculated by using a Vortex Lattice Method. Sail surface is divided into rectangular panels, and a horseshoe bound vortex is placed on each panel at a distance of 1/4 panel length from the fore end of panel. Free wake vortices proceed downstream from the trailing edge of sail. Shapes and positions of wake vortices are determined so that the wake vortices are to be parallel to the local velocity field induced by total vortex system [8].

　

 Step-by-step procedure is adopted in the present paper to determine the strength of bound vortices and the location of wake vortices, which is conducted until the calculated life and drag forces are converged. Strengths of bound vortices are determined so as to satisfy the boundary condition on the sail at the control points, which are placed on each panel at a distance of 1/4 panel length from the aft end of panel. Wake vortices are shed from the trailing edge of the sail in each time step. Strength of wake vortex is determined according to the following Kelvin's theorem.

　

　

　

 where ΓB and Γw are the total strength of bound vortices and wake vortices. Integrating Equation (20) taking account of Equation (19), total strength of wake vortex filaments at k-th time step,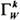, can be given by

　

　

 where 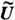is the local velocity and Δξ is the distance that a wake vortex filament proceeds downstream in a time step Δt. Superscripts k and k-1 denote each time step, Assuming that each vortex filament proceeds Δξ = 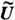Δt in a time step, the strength of wake vortex filaments can be given by

　

　

 Maintaining the vortex strength, the shed out vortex filament moves downstream at local field velocity in the direction of field velocity vector, which is updated in every time step. Once all vortex strengths are determined,lift, induced drag, aud moments acting on the sail can be calculated.

　

6.3 Comparison of Lift, Drag and Moment

　

 Sail forces and moments calculated by the Vortex Lattice Method are compared with the measured one in the wind tunnel test . Input data for the calculation are measured sail shape, apparent wind angle and apparent wind speed. Sail plane was divided into 144 panels; that is, 6 panels in vertical direction and 24 panels in horizontal direction. The mirror image of sail was taken into account about the deck plane. Number of total steps was around 40 in each calculation.

　

 Figure 12 shows the wake profile at the final step of step-by-step calculation It can be seen that the tip vortex system is well simulated. Figure 13 shows the lift, drag, and moment coefficients. Up to 30 degrees of the apparent wind angle, calculated results show good agreement with the experimental ones in the lift coefficient CL , and also in the drag coefficient CD if O.15 of the frictional drag is added. In the moment coefficient CN , there is a little discrepancy between calculated and experimental results. However, the numerical calculation showed that the Vortex Lattice Method provides good results for the square sail, although which has low aspect ratio and very large camber.