With the equations (3) and (4), the inverse Fourier transformation of the frequency response functions, the 1^st order and 2^nd order impulse response functions of wave forces are calculated.

　

　

 Here, 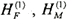is the linear frequency transfer function of 1^st order wave forces and moment respectively, and 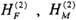is the quadratic frequency transfer function of 2^nd order wave forces and moment.

 For example, Figure 6 is the quadratic impulse response function of wave forces. Finally, the time history of the 1^st order and 2^nd order wave forces in irregular waves are calculated through the equation (5) to equation (6).

　

　

 Here, 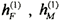is the linear impulse response function and 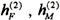is the quadratic impulse response function.

　

 Using the equation of motion in chapter 2, and with wave exciting forces gotten from chapter 3, the surge, sway and yaw motions are simulated. In the simulation, the tension of mooring line is assumed as a catenary, and the horizontal tension of the mooring line is predicted by the equation (7).

　

　

 Here, w(=0.0107kgf) is the weight of the mooring line per unit length, xa, is the distance between the attached position and the anchoring point, h is water depth. The whole length of mooring line l is assumed 4m in this paper.