導波管（Wave Guide）は図3・26に示すような中空の金属の管で、この中を電波が伝わるわけである。導波管には図のように円形導波管や方形導波管等の種類があるが、レーダーでは専ら方形導波管が使用されているので、ここでは方形導波管についてのみ述べる。

　導波管の中は中空で、前項の同軸管とは異なって、導線ではないので、2本の線によって電気を伝えるという考え方をとるわけにはいかない。導波管の中を電波がどうして伝わるかというと、ちょうどロランの電波が地球面と電離層の間を反射しながら遠方まで届くのと同じようにして伝わると考えるのが一番理解しやすいであろう。

　

　

　この場合、管の中には図3・27の（a）と（b）に示すように二つの電波が進んで行くと考える。前に図3・25で示したように電界と磁界は直交しているが、この場合は、電界は紙面に垂直に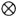（とで表示）、磁界は紙面に平行であるとする。

　

　

　こうすると、（a）（b）の両方の進行波の合成は同図の（c）のようになり、この電界と磁界が絡みあって管の中を進んでいくことになる。

　

　

　

　この図を三次元的に書いたのが、図3・28である。この図から分かるように、電界の成分は電波の進行方向にはなく、磁界は同図の（d）にあるように伝搬方向にその成分をもっている。そこで、この導波管用の伝搬モードを電気的横波（Transverse Electric Wave）、TE波と呼んでいる。あるいは、逆に伝搬方向に磁界成分があることからH波と呼ばれることもある。導波管の中での電波の伝わり方は、TE波だけではなく、その進行方向に電界成分のある磁気的横波（Transverse Magnetic Wave）、TM波またはE波と呼ばれる伝搬モードもある（図3・29（a））。更に図3・28の（b）に示した導波管の断面図では、方形面の長辺に半波長の電界分布が乗っており、短辺には電界分布がない。そこでこれをTE10波として区別する。これに対して、図3・29（b）のように長辺に一波長、すなわち電界の山が二つあるようなモードはTE20波、また、短辺と長辺が入れ変って、短辺に電界分布があるようなモード（図（c））をTE01波と呼び、このほかにも、いろいろなモードを作ることもできるが、基本のTE10波モード（図3・28）が普通に使用される。

　

　

　図3・27に戻って、導波管内では電波は斜めに進行すると考える。このとき、電波の波長λは、図3・27又は図3・30の進行方向において、その位相が360度変化する距離に相当する。しかし、導波管から見ると、導波管の長さ方向に対してλより長い距離λgで位相が360度変化することになる。このため、導波管の管壁で求めた波長を管内波長λgと呼び、λ≦λgと管内波長の方が長くなる。電波の管壁への入射角をθとすると、

という関係が得られる。この場合、導波管の中での位相の進む速度VPはVP=C/sinθ（Cは光速度）となって、光速度よりも速くなるが、これは同じ位相の点が動く速さという意味で実際の電波のエネルギーの伝送速度ではない。このVPを位相速度という。これに対して、エネルギーの伝送は群速度Vgで伝わり、これはVg=Csinθと逆に光速度により遅くなる。

　従って、VPとVgの関係は

　

　

となる。

　このように、導波管の中を斜な管壁で多重反射をしながら進む電波が、どのような斜行をするか、すなわち、θの大きさは電波の波長λと導波管の寸法aによって決まる。図3・30においてacosθ＝λ／2であるから、導波管の中をエネルギーが伝わる群速度Vgは

　

　

となり、ここでもλ≧2aになると、Vgは0または虚数となる。これは、電波のエネルギーはもはや導波管の中を伝わることができないことを示しているわけで、このような波長λ´を、遮断波長、またその波長に対応する周波数を遮断周波数という。言い換えると、方形導波管はその幅の2倍以上の波長の電波を伝えることはできないことになる。上式から、管内波長λgは、次のようにも表すことができる。