|
7・3・3 正弦波交流の複素数表示
正弦波電流
よって上式を複素数で表わす方法を考える。
先づ、この iをベクトル 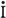 で表わせば、図7・15のとおりとなる。
図7・15
次に、これを複素数で表わすには図7・16に示す三角関数を用いることが必要である。
図7・16において、
図7・16
7・3・4 複素数の計算
(1)複素数の和
| (拡大画面:14KB) |
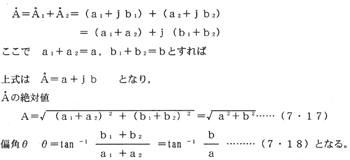 |
(2)複素数の差
| (拡大画面:10KB) |
 |
〔例題〕
(3)複素数の乗法
| (拡大画面:16KB) |
 |
それ故θ=θ1+θ2・・・(7・20)となる。
(4)複素数の除法
| (拡大画面:19KB) |
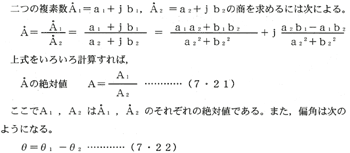 |
(5)ベクトルと虚数(j)の積
(a) ベクトル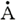 =a+jbにCを乗じた場合 =a+jbにCを乗じた場合
となり、これをベクトル図に描けば、図7・17のとおり、結局、絶対値がC倍となり偏角θの値は変化しない。
図7・17
(b) ベクトル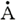 =a+jbに虚数(j)を乗じた場合 =a+jbに虚数(j)を乗じた場合
となりこれをベクトル図に描けば、図7・18のとおりとなり
絶対値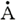 は変化しないで、偏角θがπ/2(=90°)増加し、ベクトル的にはπ/2だけ進むことになる。 は変化しないで、偏角θがπ/2(=90°)増加し、ベクトル的にはπ/2だけ進むことになる。
注:jを乗ずることはπ/2(=90°)だけ偏角が増加することであり、その角だけ進むことに注意する。
図7・18
〔例題〕
絶対値が10で偏角が30°のベクトルAに、j3を乗じたら、その絶対値A'と偏角θ'はそれぞれいくらになるか。
〔解〕絶対値は3倍になり、偏角はπ/2(90°)進むからA'とθ'は次のようになる。
A′=10×3=30、θ′=30°+90°=120°
|