|
5. 二次電源
| (拡大画面:5KB) |
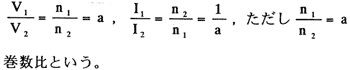 |
V1:一次端子電圧〔V〕、V2:二次端子電圧〔V〕、n11一次巻線の巻数
n2:二次巻線の巻数、I1:一次電流〔A〕、I2:二次電流〔A〕
注:一次と二次の電圧比は巻数比に等しいことに注意すること。
変圧器の容量(定格出力) P=二次定格電圧×二次定格電流
=V2×I2×10−3〔kVA〕
力率cosθは通常l00〔%〕とする。
〔例題〕200〔V〕、75〔A〕の二次側電圧、電流の変圧器の定格容量を求めよ。
〔解〕定格容量=200×75=15、000=15〔kVA〕
| (拡大画面:10KB) |
 |
V2:二次端子電圧〔V〕、I2:二次電流〔A〕、cosθ:力率(小数)
Wi:鉄損(ヒステリシス損+過電流損)
| (拡大画面:6KB) |
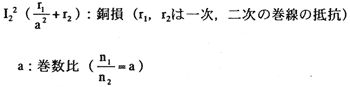 |
| (拡大画面:12KB) |
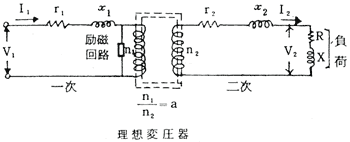 |
上図の鉄心入り変圧器を考えれば
V1、V2は一次、二次の端子電圧r1、r2は一次、二次の巻線抵抗x1、x2は一次、二次の漏れリアクタンス
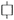 は励磁用アドミッタンス(並列に挿入されているため) aはn1/n2巻数比
このままの回路では計算が難解のため、これを次のように等価回路に置き換えて計算することができる。そうすることによって、計算が楽にできるからである。
| (拡大画面:10KB) |
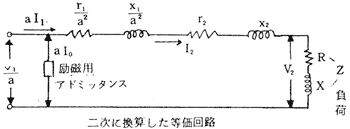 |
上図は一次を二次に総べてを換算した等価回路である。
そして励磁用アドミッタンスは電源側に移す。
そうするためには途中の計算は、省略して諸定数が次のようになる。
(1)二次に換算した諸定数
| (拡大画面:8KB) |
 |
この場合のaIoの励磁電流は小さいため無視する。
(2)一次に換算した諸定数
Ro1=r1+a2x2〔Ω〕 全等価抵抗
Xo1=X1+a2r2〔Ω〕 全等価リアクタンス
Zo1=Ro1+jXo1
=(r1+a2r2)+j(x1+a2r2)〔Ω〕 全等価インピーダンス
| 電圧変動率 ε= |
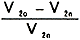 |
×100〔%〕 |
V2n:二次端子電圧(一次端子電圧を一定に保ち、指定の力率cosθ2で全負荷をかけたときの端子電圧)
V2o:二次端子無負荷電圧(上記の負荷を急に無負荷にしたとき)
以上は小型変圧器で実負荷をかけて測定するが、大型の場合はこれが不可能のため、通常二次に換算した等価回路により求める。次式がこれを示す。
| (拡大画面:4KB) |
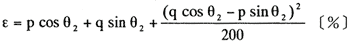 |
また、第3項を省略することができる。
| (拡大画面:13KB) |
 |
〔例題〕1. 20〔kVA〕、2,200/220〔V〕、60〔Hz〕単相変圧器の低圧側を短絡し、高圧側に86〔V〕を加えたとき、電力計の読み360〔W〕、電流計の読み10.5〔A〕を得たとし、高圧側に換算した全等価リアクタンスを求めよ。
| (拡大画面:8KB) |
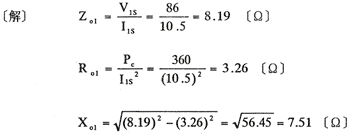 |
〔例題〕2. 例題1.の変圧器で負荷力率0.8の遅れ電流が流れたときの電圧変動率を求めよ。
| (拡大画面:15KB) |
 |
〔例題〕3. 前問において百分率抵抗降下は1.35〔%〕で、百分率リアクタンス降下は3.10〔%〕である。この場合の変圧器の力率100〔%〕及び進み力率80〔%〕のときのそれぞれの電圧変動率を求めよ。
〔解〕5・1・5項の式電圧変動率 ε=pcosθ2+qsinθ2〔%〕によって計算する。
(1)力率100〔%〕の場合
cosθ2=1、sinθ2=0であり、
またP=1.35から
ε=pcosθ2=1.35〔%〕
(2)力率、進み力率80〔%〕の場合
この場合の計算ではsinθ2を(−)にとって行う。
| sinθ2= |
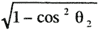 |
=0.6、またq=1.86〔%〕から |
ε=pcosθ2−qsinθ2
=1.35×0.8−3.10×0.6=1.08−1.86
=−0.78〔%〕
注:例題2及び3から同一変圧器において次のように負荷力率によって電圧変動率が変わることが理解できる。
| 負荷力率〔%〕 |
進み力率80 |
力率100 |
遅れ力率80 |
| 電圧変動率〔%〕 |
−0.78 |
1.35 |
2.95 |
|
〔例題〕4. ある変圧器で電圧比が無負荷で4:1、定格負荷で4.2:1であるという。この変圧器の巻数比と電圧変動率を求めよ。
| (拡大画面:14KB) |
 |
|