|
4・3 発電機械
(1)出力
出力P=VI×10−3〔kW〕
V:定格電圧〔V〕
I:定格電流〔A〕
(2)原動機の出力
| 直流発電機入力 PG= |
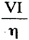 |
×10−3〔kW〕 |
η=発電機の効率(小数)
| 同上用原動機出力 PE= |
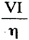 |
×10−3〔kW〕 |
(3)効率
| 諸損失: |
銅損(電機子巻線+界磁巻線) |
| |
鉄損(電機子鉄損) |
| |
摩擦損(軸受+カーボンブラシ+空気の摩擦) |
| |
漂遊負荷損(不定) |
|
(4)電圧変動率
| 電圧変動率 ε= |
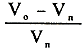 |
×100〔%〕 |
Vo:定格出力から無負荷になったときの電圧〔V〕
Vn:定格負荷時の端子電圧〔V〕
注:1. 原動機の速度変動を発電機に加えない発電機自体の変動率を固有電圧変動率といい、原動機の分を加えた変動率を総合電圧変動率という。
2. 電圧変動率試験を行うに際しては、定格負荷、定格回転数、定格電圧に調整しておき、その後は一切調整を行わないで実施する。
(5)並行運転の条件
2台以上の直流発電機を円滑に並行運転を行うためには、次の条件を満足することが必要である。
(a)原動機の調速機(ガバナー)の特性を含めた発電機の負荷電流一電圧の特性曲線が各発電機ともほぼ均一で、垂下特性であること、この場合、発電機容量は甚だしく相違しないことが望ましい。
(b)上記垂下特性はなるべく近似的であること。
(c)複巻直流発電機の場合には、次の図のように均圧線を設け、この均圧線の抵抗は母線を含めて小なることが望ましい。少なくとも発電機用主回路電線の1/2の断面積を必要とする。
| (拡大画面:21KB) |
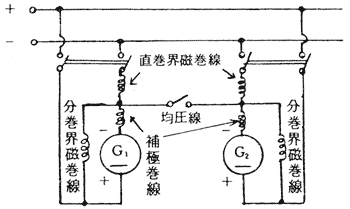 |
理由:図のように直巻界磁幹線を均圧線で接続すれば、両巻線の電流が均等に流れることをねらったものである。
そのため相互調整作用によって、負荷分担が甚だしく不均衡とならない。
注:複巻度が分巻発電機に近い程度の特性の場合には、均圧線を省略することがある。
(1)単相交流発電機
(a)出力
出力 P=VIcosθ×10−3〔kW〕
V:定格電圧〔V〕
I:定格電流〔A〕
cosθ;力率(小数)
(b)原動機の出力
| 発電機入力 PG= |
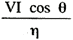 |
×10−3〔kW〕 |
η=発電機の効率(小数)
| 同上用原動機出力 PE= |
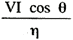 |
×10−3〔kW〕 |
(c)効率
| 諸損失: |
銅損(電機子巻線+界磁巻線) |
| |
鉄損(電機子鉄損) |
| |
摩擦損(軸受+カーボンブラシ+空気の摩擦など) |
| |
漂遊負荷損(不定) |
|
注:励磁機の損失は、主機に直結された励磁機にかぎりその機械損を主機の損失に含める。
(2)三相交流発電機
(a)出力
出力 P=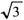 VIcosθ×10−3〔kW〕 VIcosθ×10−3〔kW〕
V:定格電圧(端子電圧)〔V〕
I:定格電流(線電流)〔A〕
θ:電圧と電流との位相角〔rad〕
cosθ:力率(小数)
(b)原動機の出力
| 発電機の入力 PG= |
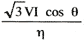 |
×10−3〔kW〕 |
η=発電機の効率(小数)
| 同上用原動機出力 PE= |
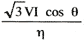 |
×−3〔kW〕 |
(c)kVA表示容量
| 皮相電力 Pa= |
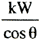 |
〔kVA〕 |
出力 P=皮相電力〔kVA〕×力率=kVA×cosθ〔kW〕
(d)交流発電機の定格容量
定格容量は通常kVA(皮相電力)で表される。
なぜならば、電機子銅損は電流で定まり、力率〔cosθ〕とは無関係であるからである。
従って、原動機との関係で出力〔kW〕というときは力率〔cosθ〕を付言しなければならない。
〔例題〕三相Y結線の三相交流発電機の相電圧1.330〔V〕相電流150〔A〕となるとき、線間電圧及び定格を求めよ。
| 〔解〕線間電圧 |
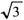 |
×1,330=2,303.5〔V〕 |
定格 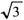 ×2,303.5×150×10 −3=598.4〔kVA〕 (e)効率
| 諸損失: |
銅損(電機子巻線+界磁巻線) |
| |
鉄損(電機子鉄損) |
| |
摩擦損(軸受+カーボンブラシ+空気の摩擦など) |
| |
漂遊負荷損(不定) |
|
これらの諸損失は電気学会電気規格調査会標準規格(JEC)などでその損失測定法が定められているので、これにしたがって測定した値を上式に算入して効率を算出する。なお、主軸に直結された励磁機にかぎり、その機械損を主機の損失に含める。
このような効率を規約効率といい、これに反して実際に負荷をかけて測定して求めた効率を実測効率という。
(f)電圧変動率
| 電圧変動率 ε= |
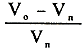 |
×100〔%〕 |
Vo:定格出力から無負荷になったときの電圧〔V〕
Vn:定格負荷時の端子電圧〔V〕
注:励磁及び速度を変更することなく、定格出力(定格力率における)から無負荷にした時の電圧変動の割合であって、発電機自体の変動率を固有電圧変動率といい、原動機の調速機の変動を加えた変動率を総合電圧変動率という。
〔例題〕三相交流発電機の定格電圧が455〔V〕で、急に無負荷にしたとき電圧が、466〔V〕になった、このときの電圧変動率を求めよ。
| (拡大画面:3KB) |
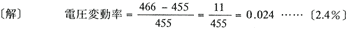 |
(g)並行運転
2台以上の交流発電機の並行運転が円滑に行われるためには次の条件が必要である。
(ii)各発電機の起電力の周波数が互いに等しいこと。
(iii)各起電力の実効値が互いに等しいこと。
(iv)各起電力の位相が互いに等しいこと。
(h)並行運転中の横流
並行運転中の交流発電機相互間に次のように流れる電流を横流といい、次に示す原因による。
(1)各発電機の起電力の大きさが等しくない場合
上図において 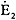 > 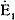 の場合には両機間に 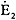 − 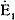 の起電力が生ずる。よって Zs:同期インピーダンス Xs:同期リアクタンス
このため図のように横流I。が流れる。
左図のベクトルのように 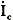 は 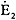 より約90°遅れ、 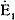 より約90°進む電流となる。 このために、G2は減磁作用となりG1は増磁作用となり起電力を高める。
そして一定の値に落ちつき、 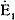 = 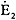 となって 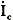 は流れなくなる。 このIcの横流を無効横流といい、無益に電機子を熱する。
(2)各発電機の周波数が等しくない場合(回転速度が一致していない場合)
両機の周波数が少し相違している発電機を並行運転すれば、両機間に横流が流れる。
左図において 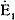 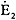 のように電圧が等しければ横流は流れないが、G 2機の速度がG 1機より速ければベクトルは 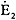 から 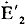 の方向に進む。 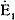 と 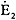 の合成電圧は 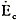 となる(上図参照のこと)、これによって 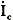 なる横流が流れる。 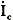 は 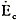 より約90°遅れて流れ、 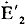 に接近する。
ただし、Zsは両機とも等しいとする。
ただし、ra<Xsとする。
G 2機は 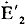 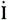 cosφなる電力をG 1機に送るので減速し、一方 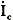 は 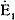 に対し位相が約180°違うので 電動機作用を生じ、G1機は加速され位相差θがなくなる。 このように、うち1機の速度が変われば直ちに横流 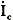 、が流れ、両機を位相差のない状態、すなわち同期の状態に引き戻そうとするので、この場合の横流を特に 同期化電流といい、この力を同期化力という。 その他、起電力の波形及び位相の相違のために悪影響があるが、ここでは省略する。
(i)交流発電機の短絡比
左図において交流発電機の無負荷飽和曲線Mにおける定格電圧に対応する励磁電流 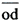 と短絡曲線sの定格電流に対応する励磁電流 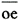 との比、 即ち 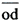 / 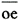 を 短絡比という。 これは重要な特性定数である。
普通この値は0.6〜15で1.0程度のものが多い。
短絡比が大きいものは、空隙が大きく機械が大きくなる。したがって高価であるが、その反面電圧変動率や安定度が良好となる。
|