|
(3)短絡電流計算例
(a)A点における短絡電流(G1+M系統)
この短絡電流の計算は発電機G2系ACB2の遮断容量を評価するために行なう。
| (拡大画面:8KB) |
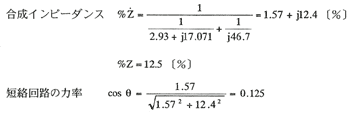 |
次の値を計算するためには、図3.2において短絡力率0.125からMP、MA、MNの値を求めてから行なう。
| 三相対称短絡電流実効値 Isym(rms)= |
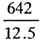 |
×100=5,136〔A〕 |
非対称最大電流尖頭値 Imax=5,136×2.37=12,173〔A〕ただしMP=2.37
非対称三相平均電流実効値 Iasym=5,136×1.20=6,123〔A〕ただしMA=1.20
非対称最大電流実効値 Iasym(rms)=5,136×1.38=7,088〔A〕ただしMN=1.38
永久短絡電流(発電機1台分) Is=642×3.5=2,247〔A〕ただし励磁用CTの飽和を3.5PUとする。
(b)B点における短絡電流(G1+G2+M系統)
この短絡電流の計算は短絡点B系統のMCB1の遮断容量を評価するために行う。
| (拡大画面:9KB) |
 |
次の値を計算するためには、図3.2において短絡力率0.144からMP、MA、MNの値を求めてから行う。
短絡電流
| Isym(rms)= |
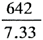 |
=8,759〔A〕 |
Imax=8,759×2.32=20,321〔A〕ただしMP=2.32
Iasym=8,759×1.18=10,336〔A〕ただしMA=1.18
Iasym(rms)=8,759×1.34=11,737〔A〕ただしMN=1.34
(c)C点における短絡電流(G1+G2+M+T系統)
合成インピーダンス % 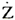 =(1.06+j7.25)+(1.7+j0.20)+(20.1+j18.8) +(0.62+j0.099)=23.48+j26.35〔%〕
%Z=35.3〔%〕
| 短絡回路の力率 cosθ= |
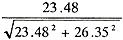 |
=0.66 |
次の値を計算するためには、図3.2において短絡力率0.66からMP、M、MA、MNを求めてから行う。
短絡電流
| Isym(rms)= |
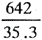 |
=1,818〔A〕 |
Imax=1,818×1.54=2,799〔A〕ただしMP=1.54
上記の値を105V電圧に変換すれば
| Isym(rms)=1,818× |
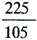 |
=3,895〔A〕 |
| Imax=2,799× |
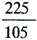 |
=5,997〔A〕 |
〔例題〕ある変電所で合成インピーダンス0.4〔%〕(10,000〔kVA〕基準)の所に布設する遮断器に必要な遮断容量〔MVA〕はいくらか。
| (拡大画面:6KB) |
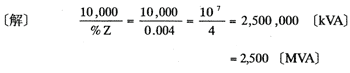 |
(1)遅れ力率0.65、三相400〔kW〕の負荷の力率を0.9に改善するに要する電力用コンデンサの容量〔kVA〕を計算によって求めよ。
(2)電圧100〔V〕の回路に力率0.55、容量330〔W〕の負荷がある。いまこれに進相用コンデンサを取付けて力率を0.85に改善した。進相用コンデンサを取付けることによって皮相電力はどれほど減少したか。
(3)三相配電線路において力率0.8(遅れ)なる240〔kW〕の三相平衡負荷がある。負荷側端子電圧3,000〔V〕、配電線1条の抵抗が3〔Ω〕、そのリアクタンスが2〔Ω〕であるとき、送電側端子電圧は何〔V〕か。
(4)電灯負荷を供給している次の図のような単相二線式低圧配電幹線ADがある。A、B、C、Dの各点の負荷電流及び負荷点問の距離は図のとおりとする。いまこの低圧幹線中の一点Fから供給するものとし、FA及びFD間の電圧降下を同一にするようなF点の位置を求めよ。ただし電線の太さはAD間を通じて一様に往復電線1〔m〕の抵抗をr〔Ω〕とし、また電線のリアクタンスは無視するものとする。
(5)配電回路の短絡電流計算方式にはいろいろあるが、目安として算定する交流回路の場合につき示せ。
|