|
3・5 配電回路における短絡電流計算
(1)直流回路
短絡電流 Is=10×(IG1+IG2+・・・+IGn)+6×(Im1+Im2+・・・+Imn)〔A〕
(2)交流回路
短絡電流 Is=10×(IG1+IG2+・・・+IGn)+3×(Im1+Im2+・・・+Imn)〔A〕
IG1・・・IGn:接続される発電機(予備機を含む)の定格電流〔A〕
Im1・・・Imn:発電機から給電をうけている運転中の各電動機の定格電流〔A〕
ただし、発電機には制動巻線を有するものとする。(現在船舶用としては制動巻線のないものはほとんど使用されていない)
〔例題〕750〔kVA〕三相交流発電機(450〔V〕、60〔Hz〕、力率80〔%〕)2台が運転中、次の三相誘導電動機(440〔V〕、60〔Hz〕)に給電している間、主配電盤付近の回路に短絡が起きたときそめ推定短絡電流を求めよ。ただし三相誘導電動機には22〔kW〕
(定格電流40〔A〕)9台、30〔kW〕(定格電流50〔A〕)4台、37〔kW〕(定格電流60〔A〕)2台及び45〔kW〕(定格電流80〔A〕)1台とする。
| 〔解〕発電機、定格電流 IG= |
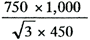 |
≒963〔A〕 |
短絡電流Is=10×(963+963)+3(360+200+120+80)
=19,200+2,280=21,480〔A〕
(1)予備知識
電気回路に電源を急に加えたとき、又は、取り去ったときには過渡現象が起こるがこれは回路定数の値に従って時間内に電圧、電流が変化し、これらは逐には定常状態になる。ここでは三相交流の配電回路に短絡電流が流れた場合の短絡電流の計算法に先立ち、三相交流発電機の短絡現象を調べてみよう。
(a)三相交流発電機の無負荷時の三相突発短絡電流
ここではa相の過渡短絡電流ιa、についての式を次に示す。ただし三相交流発電機には制動巻線を有する場合とする。
| (拡大画面:8KB) |
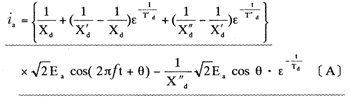 |
| |
ここで |
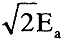 |
:a相の誘起電圧の最大値〔V〕、 |
| |
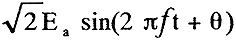 |
〔V〕 |
θ:短絡瞬時の界磁極の中心軸とa相磁化軸との位相角〔rad〕・・・短絡投入角
Xd:同期リアクタンス〔Ω〕(定常状態にあったときのリアクタンス)
X′d:過渡リアクタンス〔Ω〕(短絡直後のリアクタンスで直軸分に対するもの)
X″d:初期過渡リアクタンス〔Ω〕(最初の突発電流の交流分を制限するもので、直軸分に対するもの)
T″d:短絡初期過渡時定数〔S〕
T′d:短絡過渡時定数〔S〕
Td:電機子時定数〔S〕
ε:自然対数の底=2.718
そしてa相の電流iaのほか、b相、c相の電流ib、icはそれぞれθの代わりに(θ−2π/3)、(θ−4π/3)を代入すればよい。
(b)時定数(じていすう)と三相交流発電機の短絡電流波形
(i)時定数とは過渡電流が時間の経過とともに変化する有様を表す定数で、回路のL、R、Cなどに関係する。
例えば、上図において初めに電源スイッチS1を閉じておいて、t=0でS1を開き同時にS2スイッチを閉じた場合Lに貯えられたエネルギーの電流iの状態を計算すれば次のようである。
ここでi:t秒後における電流〔A〕
I:E/Rで、のときの電流〔A〕
T:時定数といい、この場合L/Rである〔s〕
ε:自然対数の底=2.718
この式で電流の変化を表せば次図のようになる。
またt=T秒後における電流iは上式から
i=I/ε=I/2.718=0.368I〔A〕
となる。このことは電流の最初の値から36.8%に減衰するにはT秒間を要することを意味し、このT秒を時定数と称す。この時に実用的には過渡状態が終わったとみなすことができる。そこでこの時定数の逆電流の減衰波形数すなわち1/Tを減衰定数という。
(ii)交流発電機の短絡電流波形
| (拡大画面:18KB) |
 |
第2及び第3項式は、それぞれ時定数T′d及びT″dをもった指数関数曲線にしたがって、数サイクル以内に減衰する交流分である。その中で、第3項式は交流分の電機子反作用が最初に働き、制動巻線による初期過渡時定数T″dに従って急激に減衰し、次に、第2項式では電機子反作用が影響する界磁回路の時定数Tdに従って徐々に減衰する交流分であるが、最後には、第1項式のXdで電流が制限される持続電流となる。
第4項式は短絡瞬時に磁束鎖交数を一定に保とうとするための電機子に流れる直流分であって、時定数Tdに従って減衰しその初値は、次に述べるθの値によって異なる。
第1:短絡が、θ=0すなわちa相の磁束鎖交数が最大で、誘起電圧e=0の時に起こった場合、直流分の初値はt=0のとき、
| (拡大画面:7KB) |
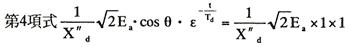 |
| |
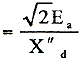 |
となり、このとき直流分は最大値となる。 |
| |
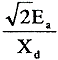 |
(第一項式)とほぼ同一であるから、 |
| |
合成短絡電沸の初振幅は最大で、その最大値は半サイクル後に起こる。 |
| |
その値は約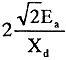 と考えられる。 と考えられる。 |
| |
第2:短絡が、θ= |
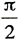 |
、すなわち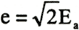 の時に起こった場合には、 の時に起こった場合には、 |
| |
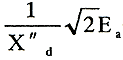 |
・cosθ・ |
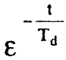 |
=0となり、このとき直流分は消える。 |
|
| |
したがって、合成短絡電流iaの初振幅は最小値で |
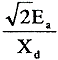 |
となる。 |
第1及び第2以外の場合の初振幅は、上記の二つの場合の中間値となる。第1の場合について図示すれば、次図のようになる。
| (拡大画面:25KB) |
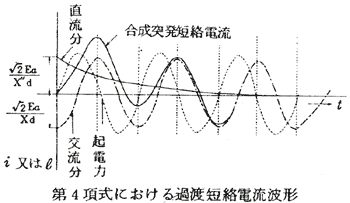 |
備考:上記の突発短絡電流の式は43ページで示したとおり、制動巻線がある場合であるが、これが無い場合にはXd″=Xd′と考えられるから、第3項式は消去してよい。
下図は総合短絡電流の波形を示す。
| (拡大画面:25KB) |
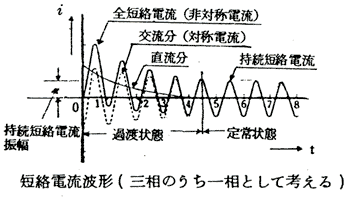 |
備考:直流分を含んだ短絡電流を非対称短絡電流といい、これを含まない電流を対称短絡電流という。
|