|
7・3・4 複素数の計算
(1)複素数の和
二つの複素数  1 1=a 1+jb 1、  2 2+jb 2の和を求めるには次による。
 =  1 1+  2 2=(a 1+jb 1)+(a 2+jb 2)=(a 1+a 2)+j(b 1+b 2)
ここで a1+a2=a、b1+b2=bとすれば
上式は  =a+jb となり
| (拡大画面:4KB) |
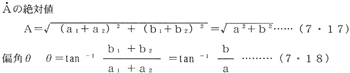 |
となる。
(2)複素数の差
二つの複素数  1 1=a 1+jb 1、  2 2=a 2+jb 2 の差は上記の(1)にならって、それぞれの差を求めて計算をする。  =  1 1−  2 2, a=a 1−a 2, b=b 1−b 2,  =a−jb
〔例題〕
 1 1=7+j6、A 2=3+j4 において  1 1と  2 2で表示される二つのベクトルの差を求め  を描け。 〔解〕  =  1 1−  2 2=7+j6−3−j4=4+j2となり、これをベクトル  は次のようになる。
(3)複素数の乗法
二つの複素数  1 1=a 1+jb 1、  2 2=a 2+jb 2の積を求めるには、次による。  =  1 1 2 2=(a 1+jb 1)(a 2+jb 2)=(a 1
a 2−b 1 b 2)+j(a 1
b 2+a 2 b 1)
また、  1 1、  2 2で表されるベクトルの偏角をそれぞれθ、θ 1、θ 2とすれば tan θ=tan (θ1)+θ2
それ故 θ=θ1+θ2・・・(7・20)となる。
(4)複素数の除法
二つの複素数  1 1=a 1+jb 1、  2 2=a 2+jb 2の商を求めるには次による。
| (拡大画面:5KB) |
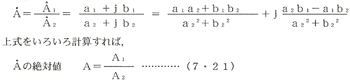 |
ここでA 1、A 2は  1 1、  2 2のそれぞれの絶対値である。また、偏角は次のようになる。 θ=θ1−θ2・・・(7・22)
(5)ベクトルと虚数(j)の積
(a)ベクトル =a+jbにCを乗じた場合 =a+jbにCを乗じた場合
 '=C  =C(a+jb)=Ca+jCb・・・ (7・23)となり、これをベクトル図に描けば、図7・17のとおり、結局、絶対値がC倍となり偏角θの値は変化しない。
図7・17
(b)ベクトル =a+jbに虚数(j)を乗じた場合 =a+jbに虚数(j)を乗じた場合
 '=j  =j(a+jb)=ja+j 2b=−b+ja・・・ (7・24)となりこれをベクトル図に描けば、図7・18のとおりとなり
図7・18
〔例題〕
絶対値が10で偏角が30°のベクトルAに、j3を乗じたら、その絶対値A’と偏角θ’はそれぞれいくらになるか。
〔解〕
| (拡大画面:4KB) |
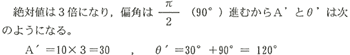 |
|