|
第2章 船体強度
2.1 材料力学の基礎
2.1.1 荷重、応力、ひずみ、ヤング係数
物体に外から働く力を外力といい、これに対して自身の重さとか、運動していることによって生ずる慣性力(加速度に比例する)を内力という。これら外力と内力とを合わせて荷重といい、物体を変形させたり、破壊させたりするもととなる。単位はkgかtonを用いる。物体に与える変形のもようによって荷重を分けると、引張、圧縮、せん断、曲げ、ねじり、などの種類になる。
荷重に加わると、物体の内部にこれに抵抗して応力が生じる。応力は単位面積当りの力の形で表わし、kgf/mm2(N/mm2)などの単位が用いられる。さきに述べた鋼材の強さもこの応力を単位として表わしている。単位面積当りにするのは、いろいろ寸法の異なった場所での比較に便利なためで、土地の価格や建築費を坪当りとか、m2当りとかであらわすのと同じである。
応力によって物体の形は変化する。たとえば、引張り応力を受けると伸び、曲げ応力を受ければ曲がる。この変化量ともとの寸法との割合をひずみ(歪)という。この場合は単位長さ当りの変形長さでcm/cm、mm/mmのように表わせる。普通非常に小さい値(百万分の1から千分の1まで位)なので、×10-6(百万分の1単位)または×10-3(千分の1単位)と書き、cm/cmは省略する。
前章の1.3で鋼材について説明したときに、縦軸に応力を、横軸にひずみを取って表示したが、これを応力−ひずみ曲線という。鋼材では弾性限度内(正確には比例限度内)では、応力が2倍になれば、ひずみも2倍になるように応力とひずみは比例している。この比例常数をヤング係数(応力をひずみで割った値といってもよい)という。単位は応力の単位と同じで、ただ数字は大きい。鋼材のヤング係数は21,000kgf/mm2(205,940N/mm2)で、鋼材の種類によらずほぼ一定と考えてよい。
(1)引張
いま、第2.1図のような丸棒の両端を、図のように引っぱれば、長さが長くなって太さが細くなる。
第2.1図
このような荷重を引張荷重あるいは引張力といって、この場合、棒の両端に働く二つの力Pは必ず同じ大きさで、その方向は反対である。この二つの力Pを受けた棒の中には、どこで切ってもPと同じ大きさの引張力P1とP2とが向かい合って生じて、力を他の部分に伝えている。
いま、任意のところにXX断面を考えて、その断面積をamm2、荷重Pkgとすると、単位面積に働く引張応力Stkgf/mm2(N/mm2)は
St=引張荷重/断面積=P/a (1)
で表わされる。
(2)圧縮
圧縮は、引張の反対で、棒の両端を押すので、長さが短く、太さが太くなる。このような荷重を圧縮荷重あるいは圧縮力といい、棒の内部に生じる応力を圧縮応力という。
圧縮応力Scは
Sc=圧縮荷重/断面積=P/a (2)
で表わされる。
(3)せん断
第2.2図は、2枚の鋼板をリベットでとじたものである。この板の両端を図のように引っぱると、リベットはYY面で、はさみで切るように上下の部分が別々に左右に滑りだそうとする。
第2.2図
このような荷重をせん断力といい、このときにリベットの内部YY断面に生じる応力を、せん断応力という。
いま、リベットの断面積をamm2、せん断力をPkgとすると、せん断応力Sskgf/mm2(N/mm2)は
Ss=せん断力/断面積=P/a (3)
で表わされる。
(4)曲げ
上に述べた引張・圧縮・せん断力では、荷重と応力とは比例しているから、たとえば荷重を倍にすれば応力も倍となる。ところが、曲げの場合は少し様子が違う。
第2.3図
たとえば、第2.3図の棒の一端に荷重Pをかけたとき、その曲がり方は荷重Pによって決まるのではなくて、Pに支点からの距離をかけた曲げモーメントP×lによって決まるのである。
船体各部の寸法も同じように船体にかかる荷重だけでなく、曲げモーメントによって決める場合が多い。
簡単のために、第2.4図のように、両端を支えられた長方形断面の棒が中央に垂直荷重を受けて、図の下のように曲がったとする(このように機械や構造物の長さの方向に直角に力を受ける部材を一般に、はりまたはビームという)。
そうすると、はりの上面は圧縮を受けて縮み、下面は引張を受けて伸びる。したがって、はりの深さの中ほどに、伸びも縮みもしない層があるはずで、この層を中立軸という。
このときの引張応力あるいは圧縮応力は、中立軸に近いほど小さく、遠いほど大きいからこれを図に表わせば第2.5図のようになるはずである。
この図のように、曲げによって生じる垂直応力を特に曲げ応力という。
第2.4図
第2.5図
2.1.2 はりの種類
はりに曲げが作用しているとき、はりを支えている点を支点といい、両支点間の距離をスパンという。はりは、支持する方法によって第2.6図に示す6種類がある。
| (拡大画面:14KB) |
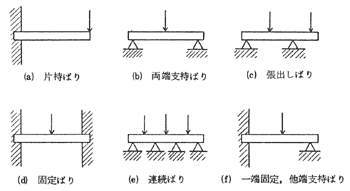 |
第2.6図 はりの種類
(1)片持ばり
図(a)のように、一端が固定されているはりである。固定されているほうの端を固定端、自由なほうを自由端という。
(2)両端支持ばり
図(b)のように、両端が自由に動くように支持したはりで単純ばりともいう。
(3)張出しばり
図(c)のように、支点の外側に荷重のかかるはりで、支点から荷重までの距離のことをオーバーハングという。
以上三つのはりは、支点の反力を力のつりあいから求めることができる。
(4)固定ばり
図(d)のように、両端が固定されているはりである。両端は水平方向にも動けず、回転もできずに固定されているので、はりの中で最も強いものである。
(5)連続ばり
図(e)のように、3点以上の支点で支えられたはりである。
(6)一端固定、他端支持ばり
図(f)のように、一端が固定された支点で、他端は両端支持ばりのときの支点と同じもので支えられているはり。
以上の三つは、はりの変形も考えて解かなければならないはりである。
船体の構造物は、たゆみ性があるので、完全な固定端にはならないが、強固なブラケットを使えば、固定端に近い状態が得られ、同時にビームのスパンが実質的に短くなる。
また、船の場合は等分布荷重( 次項参照)が大部分である。このような等分布荷重を受ける固定端ビームにおいては、最大曲げモーメントは両端部に生じて中央部の2倍に達するから、ビームが弱くて折れるような場合には、端部から折れる。ビームの両端部にじょうぶなブラケットを必要とするのは、このような理由があるからである。 |