|
SIMULATION
Figure 9 shows the bathymetry of Naari beach. We took the computation area of the wave model up to the water depth of about 40 m where the bottom contour line is almost straight in the north-south direction. Both Δx and Δy were 30 m so that 110 and 113 grid points were used in x- and y -direction, respectively. Constant (but changing with time) wave heights and directions were assumed along the offshore boundary. Figure 10 shows an example of the distribution of wave heights normalized with respect to the incident wave height and the wave direction vectors computed by the wave model. In the lee of the intake breakwaters where wave diffraction is dominant, the wave heights are small and the wave directions change significantly.
| (Enlarge: 30KB) |
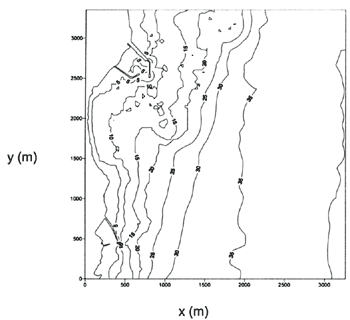 |
Figure 9. Bathymetry of Naari beach
| (Enlarge: 47KB) |
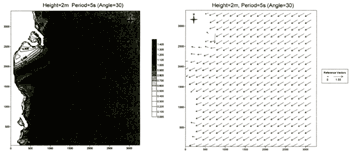 |
Figure 10. Example of computational results of wave model
| (Enlarge: 11KB) |
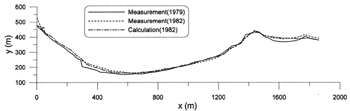 |
Figure 11. Comparison of measurement and calculation of shoreline change
The initial shoreline was discretized by 10 m in x -direction. The north end of the beach is blocked by the intake breakwater of the nuclear power plant and the south end is blocked by the breakwater of a fishery port (Fig.9). Therefore, the boundary conditions of no flux of sediment were imposed at both ends of the shoreline. The mean diameter of the bottom sediment was 1.71 mm (Korea Electric Power Company, 1994), indicating coarse sand. The depth of profile closure is calculated to be 11.3 m using the formula proposed by Hallermeier (1983):
where (Hs)max is the maximum significant wave height during the simulation period and ss is the specific gravity of sediment relative to fluid. K1 = 0.6 and K2 = 0.1 were used.
Figure 11 shows the comparison between measurement (using aerial photographs) and calculation of the shoreline change during the first three years after the construction of the intake breakwaters. A good agreement is observed between measurement and calculation, even though there are small deviations in several places.
CONCLUSIONS
We analyzed the shoreline change of Naari beach due to the construction of intake breakwaters of the Wolsung Nuclear Power Plant using aerial photographs taken almost every five years before and after the construction of the nuclear power plant. It was found that significant shoreline change occurred during the first several years after the construction of the intake breakwaters whereas only minor change occurred afterwards, indicating that the shoreline change was caused by the construction of the intake breakwaters.
A curvilinear-coordinate shoreline evolution model combined with the Cartesian-coordinate RCPWAVE model was used to simulate the shoreline change during the first three years after the construction of intake breakwaters. A reasonable agreement was observed between the calculated shoreline change and the measured one by the aerial photographs.
Finally we could conclude that the aerial photographs could be used for the long-term monitoring of the shoreline change and the numerical shoreline evolution model as a fairly accurate tool for the prediction of the shoreline change due to the construction of coastal structures.
REFERENCES
Ebersole, B.A., M.A. Cialone and M.D. Prater. 1986. Regional coastal processes numerical modeling system Report 1 RCPWAVE - A linear wave propagation model for engineering use. Technical Report CERC-86-4. Coastal Engineering Research Center. Waterways Experiment Station, Corps of Engineers, Vicksburg, Mississippi, USA.
Hallermeier, R.J. 1983. Sand transport limits in coastal structure designs. In Conference on Coastal Structures '83. 703-716.
Korea Electric Power Company. 1994. A study on the reduction of thermal discharge effects around nuclear power plants - Wolsung. Report No.92-802 (in Korean).
Oh, Y.T. 2002. Curvilinear coordinate shoreline change model combined with finite-difference wave transformation model. Master's thesis. Seoul National University, Seoul, Korea.
Ozasa, H. and A.H. Brampton. 1980. Mathematical modelling of beaches backed by seawalls, Coastal Engineering. 4:47-63.
Suh, K.D. and S.C. Hardaway. 1994. Calculation of tombolo in shoreline numerical model, In 24th International Conference on Coastal Engineering, edited by B. Edge, 2653-2667. Kobe, Japan.
|