|
INFLUENCE OF SUBMERGED BREAKWATER TO WAVE RUNUP ON STEP DIKE
Jea-Tzyy Juang1, Chao-Fu Lin2 and Chi-Da Huang2
1Department of Environmental Engineering, Fooyin University
Taliao, Kaohsiung County, TAIWAN
jtjuang@mail.fy.edu.tw
2Department of Hydraulic Engineering, Fonchia University
Taichung City, TAIWAN
ABSTRACT
Submerged breakwater was the structures that normally constructed with rubblemound
and it has a submerged crest depth below the sea water level. It was well suited to maintain a moderate
degree of energy transfer from the offshore to the shoreline region. In this study, the wave runup theorem
which proposed by Cross and Sollitt (1972) was quoted for analysis first.
After that, based on the results of the wave runup test by the incident irregular wave, the coefficients
in the wave runup equation of the runup profile can be estimated. At the second, the computation method
for the calculate of the wave energy loss coefficient in wave runup on sea dike as well as the energy
loss of the incident wave pass over the submerged breakwater was proposed. At last, by advantage the result
of the experiment of wave runup, a prediction model for the wave runup height was proposed too. Comparison
of the result of the predicted wave runup height that obtained by the proposed calculation model and the
wave runup height that measured from the experiments was coinciding each other very well.
INTRODUCTION
The offshore structure likes the submerged breakwater was used to reduce the incident wave energy as well as the incident wave height then can achieve the purpose of coastal protection work. Meanwhile, in order to reduce the wave runup height, a series of study work on decrease down the wave runup height on sloping dike was completed at the past time. One of the ways was to construct the step dike to increase the roughness on the sloping dike surface. Based on the above-mentioned reason, the combination of the submerged breakwater and the step dike to reduce the wave runup height for protect the coastline was conducted in this study.
LITERATURE REVIEW
Seabrook and Hall (1998) proposed a calculation formula for calculate the transmitted coefficient Kt) of the waves pass over a submerged breakwater as follows.
| (Enlarge: 5KB) |
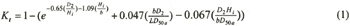 |
| where |
D2 |
: the submerged depth of the crest of submerged breakwater |
| |
Hi |
: incident wave height |
| |
L |
: incident wave length |
| |
b |
: crest width of the submerged breakwater |
| |
D50a |
: medium diameter of the armor layer |
Van der Meer and Stem (1992) according the experiment
data of the wave runup on smooth surface dike that completed by Ahren in 1981 and their own experiment
data of the run up experiment on a rubble mound dike to regress out the correlation equation between the
relative wave run-up height and the surf parameter as follows:
in which ξp called the surf parameter and Tp was the peak period. Ru2% was the averaged value of the largest 2% runup wave height.
For the calculation formula of the runup wave height, if the peak wave period (Tp) was instead by the mean wave period (Tm) for analysis then the correlation equations will be changed as follows
THEORETICAL ANALYSIS
The calculation of the runup wave profile
Cross and Sollitt (1972) proposed a calculation
formula to compute the wave runup profile (Fig.1) on a sloping dike as follow
Y=MXN-A (6)
In which X, Y was the two-dimensional coordinate. A was the wave amplitude at the trough of the runup wave that in front of the smooth sloping dike.
A=Ai+Ar=Ai(1+Kr) (7)
where Ai was the incident wave amplitude and
Kr was the refraction coefficient. Yamamoto
et. al. (1994) proposed a correlation formula of Ai and the incident
significant wave height Hsi as Ai =
0.471 Hsi. Therefore, the above equation becomes A=0.471Hsi・(1-Kr) (8)
In advance, divide both sides by A in equation (6) can obtained
Let y, r =Y/A, R/A, and x, x1 =X/LR, X1/LR, then Figure 1 can changed to the dimensionless equation as shown in Figure 2. Meanwhile, the above equation becomes
y=(r+1)xN-1 (10)
Fig.1 Wave runup
Fig. 2 Wave runup(dimensionless)
From Figure 2 we can understand
Substitute equation (10) into (11) can obtained
There have two boundary conditions. The first one was when X = X1 then Y = 0. After substitute it into equation (6) can obtained
The second one was when X = LR then Y = R, In this case, equation (6) becomes
LR=X1・(r+1)1/N (15)
Substitute equation (14) into (15), we can obtain
LR=X1(r+1)1/N (16)
Again, substitute equation (16) into (12) can obtained the following equation
Use the above equation and the experimental data, due to A, X1, R can be measured from the experiment, so that we can compute the N value. After that, use equation (14), the value of M can be calculated out also.
|