|
CALCULATION OF THE TSUNAMI SUFFERING PROBABILITY
Monte Carlo method
Figure 3 shows the flow of the Monte Carlo method for the calculation of the tsunami suffering probability. The tsunami calculation was considered random tidal height, latitude, longitude, vertical fault deformation and calculative accuracy. The iterative calculations were carried out at 5.000 times. The random data were changed on every cycle.
Figure 3. Flow of the Monte Carlo method
1) Tidal height
Only the astronomical tide was considered. Main four tidal waves (M2, S2, K1, O1) were used for tidal height. The random date was chosen every cycle of iterative calculation. The sea level discrepancy from normal at the Muroto-misaki cape were picked up.
2) Location (longitude and latitude)
At Nankaido, 34 historical earthquakes are recorded. The maximum magnitude is 8.4. The location of seabed displacement is distributed around Nankai trough. Figure 4 shows the distributions of longitude and latitude. The shapes both of them were nearly a normal distribution. We assumed the distributions as below Table 1.
Table 1. Distribution of the historical earthquake locations
| |
Distribution |
Average |
Standard deviation |
| Longitude |
Normal |
East 135.54 |
1.37 |
| Latitude |
Normal |
North 33.72 |
0.52 |
|
| (Enlarge: 21KB) |
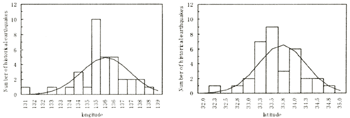 |
Figure 4. Distributions of historical earthquake epicenters
3) Earthquake magnitude
An extreme statistics analysis was carried out on the 34 earthquakes that occurred in the offshore Nankaido. The earthquake magnitude fits well with a Weibull distribution (k=2.0). As a result, we presumed the probability of the occurrence of an earthquake of M8.0 to be 100 years, and M8.4 to be 180 years. This presumption is very close to the occurrence interval of huge tsunamis at Nankaido (Table 2).
Table 2. Historical earthquakes at Nankaido(The earthquake magnitude is near or over 8.0)
| Historical earthquake |
Earthquake Magnitude |
Occurrence year (BC) |
Interval |
| Shohei |
M8.4 |
1361 |
- |
| Meio |
M8.6 |
1498 |
137 |
| Keicho |
M7.9 |
1605 |
107 |
| Hoei |
M8.4 |
1707 |
102 |
| Ansei |
M8.4 |
1854 |
147 |
| Showa |
M8.0 |
1946 |
92 |
|
We introduced various magnitudes into the tsunami calculation in the Monte Carlo simulation in the following way. First, the fault model is used for tsunami calculation. Second, the fault Area is fixed, and only the vertical fault deformation is changed. Third, the vertical fault deformation corresponding to each of the randomly chosen earthquake magnitude is acquired by complementing the vertical fault deformation of Showa earthquake (M8.0) and Ansei earthquake (M8.4).
4) Calculative accuracy
Figure 5 shows the comparison of height between trace data to calculation result at around Nankaido. It is impossible to reproduce perfectly the traces of tsunami height by calculation. We must consider that the tsunami calculation is certain to include these errors. The calculation error of the tsunami propagation calculation is readjusted by "trace height / calculation height". Figure 6 shows them. The ratio of trace height to calculation height becomes close to a normal distribution with a mean value of 1.04, and its standard deviation is 0.26.
| (Enlarge: 35KB) |
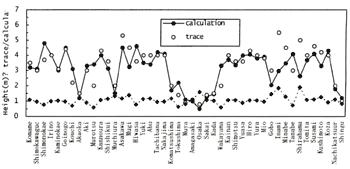 |
Figure 5. Comparison of height between trace data to calculation result
Figure 6. Distribution of the calculative accuracy
Cases of the consideration
We will examine on the case of the tsunami breakwater under construction at Asakawa bay. The tsunami propagation calculation was carried out on the six cases below each with different opening widths (Table 3). Case-1 (width=100) is a condition within both the south and north tsunami breakwaters have been completed. Case-5 (width=500) is a present condition. Only the tsunami breakwater on the south side has been completed. Case-6 (width=860) is a non-breakwater condition.
Table 3. Cases of the consideration
| Case |
Width of bay mouth |
Tsunami breakwater length
at north side |
Tsunami breakwater length
at south side |
| Case 1 |
100 m |
360 m (completed) |
400 m (completed) |
| Case 2 |
200 m |
260 m (under construction) |
400 m (completed) |
| Case 3 |
300 m |
160 m (under construction) |
400 m (completed) |
| Case 4 |
400 m |
60 m (under construction) |
400 m (completed) |
| Case 5 |
500 m |
0 m (non breakwater) |
400 m (completed) |
| Case 6 |
860 m |
0 m (non breakwater) |
0 m (non breakwater) |
|
Distribution of the tsunami height in the Asakawa bay
The output points of the tsunami calculation must be in front of the existing breakwater (Fig.3). Figure 7 shows a distribution of tsunami height which is composed of 5,000 times iterative calculation. Case-1 is the narrowest width of the bay mouth. Over half of the 5,000 calculation results are under 50 cm. While in case-6 that is non-breakwater condition, a lot of tsunamis become 1.0 to 3.0 in the bay. When the earthquake magnitude is over 8.0, the tsunami height becomes more than 5.0 meters. Compared Case-1, peak of the distribution shift more high risk.
| (Enlarge: 30KB) |
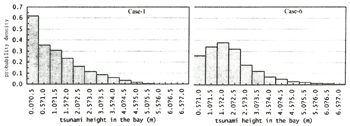 |
Figure 7. Distribution of tsunami height in the Asakawa bay
Tsunami suffering probability
In this study, "the tsunami suffering probability" is defined as the tsunamis it overtopping the crown height (=5.0 m) of the existing seawall at Asakawa bay divided by the times of repetition (=5000).
Figure 8 shows the tsunami suffering probability each case. At the present tsunami breakwater condition, we cannot expect the effect to decrease tsunami energy. Thus, the risk of tsunami disaster will be underestimated. At the districts where the tsunami breakwater is under construction, the government should reconsider the hazard map and evacuation plan. When the allowable tsunami suffering probability is fixed, the best length of the tsunami breakwater can be decided simply.
| (Enlarge: 19KB) |
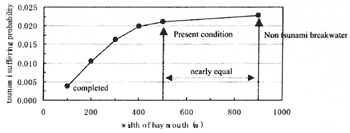 |
Figure 8. Tsunami suffering probability
|