|
NEW GRIDDED DIGITAL BATHYMETRY FOR THE KURIL-KAMCHATKA REGION
Andrei G. Marchuk1, Anatoly Yu. Bezhaev1 and Nikolay I. Seliverstov2
1Institute of Computational Mathematics and Mathematical Geophysics
Siberian Division, Russian Academy of Sciences, Novosibirsk. RUSSIA
mag@omzg.sscc.ru
2Institute of Volcanology, Far Eastern Division, Russian Academy of Sciences
Petropavlovsk Kamchatsky, RUSSIA
ABSTRACT
In the paper the algorithms and some interface for creating detailed digital regular gridded bathymetry using digital soundings data are described and examples of obtained data for different regions of the Pacific are shown. In calculations of the depth at each grid point, the algorithm uses up to 9 points from data source. They are chosen using two criterions: the first - they must be situated in various sectors (N, NE, E, SE, S, SW, W, NW) from calculating grid-point, and the second - they must be the nearest ones to this point in each sector. Then the spline interpolation is used for defining the depth value in the grid-point. Another algorithm uses linear interpolation for obtaining depth value in the grid-point. The new digital bathymetry on the rectangular grid with 1 and 0.5 arc minute resolution has been created for the Kuril-Kamchatka region. These data consist from four rectangular arrays of depth, which cover 200 km zone around the Kuril Islands and Kamchatka from 41.00°up to 61.00°Northern latitude.
INTRODUCTION
Numerical modeling of different oceanologic problems and natural hazards in
ocean now is widely used. For such a modeling (for example tsunami waves propagation) the detailed digital
bathymetry on a regular grid is required. Now no global gridded bathymetry database with resolution better
than five geographical minutes is available for users. Therefore for modeling local tsunamis (or another
hazard) it is necessary to obtain somewhere or create detailed digital bathymetry for the regarded area.
There are few ways to create such data arrays. There are several bathymetry information databanks now
are available for use. One of them is a global database "Marine Trackline Data" of depth's soundings from
the vessels (Marine Geological and Geophysical Data from NGDC) that had been collected during a very long
period (from the beginning of 20-th century), In some coastal areas location of points from this data
set are so dense, that using only this data make it possible to create the regular array of depths with
a rather small spatial step (less than one geographical minute). In the areas, where it is not enough
points with such a data, it is necessary to take into account additional information about bottom relief.
Another possible information about ocean bathymetry is the isolines of depth. The database of depths isolines
"GEBCO" (General Bathymetric Chart of Ocean) ( GEBCO 97, 1997) is the most
known global digital database, the quality of which is of no doubts. However, the set and density of isolines
are rather different for various regions. In the areas, where these isobaths together with echo sounding
data of depth cover regarded area with enough densely without "white pots", it is possible to create digital
bathymetry of high quality. In those areas, where density of Trackline and GEBCO data is seems to be insufficient,
it is necessary to input into computer the isolines of depth and spot data from available bathymetric
charts (navigating, fishing or specially prepared). Then the program that developed by the authors can
produce the detailed digital bathymetry on the regular grid.
POSSIBLE WAYS FOR CREATING GRIDDED BYTHYMETRY
At first we shall consider what kind of information can be used as a source
for crating the digital bathymetry on a regular grid. On the bathymetric maps the information about depths
is presented as isolines and dot data of depth soundings. A lot of soundings have been collected in a
digital form in the databases "Marine Tracking Data" (Marine Geological and Geophysical Data from NGDC)
and "Hydrographic Survey Data" (Hydrographic Survey Data, CD-ROM data set). This base contains the data
about measurements of depth during cruises of large number of vessels and covers with the data with a
various density practically all regions of world ocean. Each element of this database represents trace
of a vessel movement (track), along which with a very small step (about hundreds of meters) the values
of measurements of depth are presented. In some coastal regions tracks and the soundings are located so
close to each other, that only these data would be enough for creation of the regular array of depths
with a rather small step (less than one geographical minute). However, in other regions the distances
between tracks are so big, that if we take into account only this kind of bathymetry information, it would
be insufficient for creating of the qualitative detailed digital bathymetry on a regular grid. Isolines
of depth had been collected in another global bathymetric database "GEBCO" ( GEBCO
97, 1997), where some isolines of depth are stored in a digital vector form. This database covers
all regions of World Ocean. The set of isobaths values in this database depends on region, and alongside
with water areas, where this set is rather rich (in the Mediterranean sea, for example it consists of
about 40 values), there are also regions, where density of these isolines is insufficient. Also it is
possible to find some other data about depth measurements that is now not available for a wide range of
the users.
Here we shall describe some ways of creating of the arrays of depths on a regular grid using available bathymetric data. These arrays then can be used for mathematical simulation of processes in ocean. David Sandwell made the attempt to use for a gridded digital bathymetry creating the gravimetric data obtained from a satellite (Smith and Sandwell, 1997). Using this kind of data and the depth sounding data, he has constructed global two-minute gridded digital bathymetry. However, the matching of the Sandwell's data with more reliable bathymetic data in the northern Kamchatka region has revealed significant (in some places) mismatch of that data with real depths. Moreover the trackline data in some coastal regions is not well correlates with bathymetry obtained on the base of the analysis of a gravimetry. In figure 1 the fragment of the Sandwell's digital bathymetry that covers the region of central Japan and surrounding water areas is presented. The traces of vessel cruises (when the measurements of depths were made) can be clearly seen on the bottom surface (almost all of them are converging in region of the Tokyo bay). In deep-ocean areas Sandwell's digital bathymetry is sufficient for modeling ocean processes.
 Figure 1. 3D shaded image of the Sandwell's relief around central Japan
area
RECALCULATING RANDOMLY DISTRIBUTED DEPTH SOUNDINGS TO THE REGULAR GRID
Let's describe the technology of creating of the gridded digital bathymetry in case, when the points of depth sounding enough densely cover regarded area. On the first step it is necessary to choose from the whole database "Marine Trackline Data" a subset of points that are located in considered area. That will be the file, each string (line) of which consists of three numbers: longitude, latitude and measured depth. Then we must decide, what there will be a length of a step between grid points, where the depth values will be found. The last stage of the creating process will be execution of the program of recalculation of the randomly distributed depth data (depth soundings) to regular rectangular grid.
Firstly let's describe the recalculation algorithm, which uses the linear interpolation. The program considers one by one all our new grid-points. For every grid-point it is necessary to define it's geographical coordinates. Then we look through all points of the depth measurements finding distances from the considered grid-point up to each of them. If among them there is one or several points located closer, than one twentieth part of the new grid step length, then the value of depth in that grid-point is assumed to be equal to the depth value in the nearest point. If the Trackline database does not contain points, located to a new grid-point closer, than established distance, then let's take from it's (grid-point) nearest neighborhood three such points from the database, that considered grid-point is located inside the triangle formed by these three points. Then, using known values of depth in these three points with the help of linear interpolation the value of depth in a considered grid-point can be defined. As the variation of this method it is possible to estimate the depth value in a grid-point using six nearest soundings, which are located in different sectors of Cartesian coordinate system with center in the regarded grid-point. So, considering one by one all points of a new regular grid, we shall find approximate values of depth in each of them. It is obvious, that the better densely coverage of the area by soundings provided the higher quality of the being created gridded digital bathymetry.
Another method is based on the more complicated interpolation method by radial functions. Proposed method uses up to nine points from data source. One point is the nearest one among all. The other eight points are chosen using two criterion's: the first - they must be situated in various sectors (between N, NE, E, SE, S, SW, W, NW directions) of Cartesian coordinate system with the center in regarded grid-point, and the second - they must be the nearest ones to this point in each sector. When the algorithm takes into account more that one point in each sector, the quality of gridded data will be better, but computations will take much more time and resources. In this case some procedures for optimizing calculation process are proposed.
The Green's function method, which is the special case of the radial functions method, is used for depth interpolation in grid-points. Let's notice that this method is exact on linear functions. The essence of method is in choosing of one dimensional radial functions f(R). Then the linear combination
represents two-dimensional function. Here 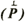 =(x,y) =(x,y)
is an arbitrary point of the area, 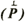 (i)=(x(i),y(i)) (i)=(x(i),y(i))
are interpolating points from different sectors. Coefficients α(i), a, b, and c are to be defined from
interpolating conditions (the coincidence of the function 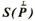
and sounding values d(j) in points 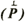 (i) (i)
which are used for interpolation
and orthogonality conditions:
From system of equations (2) and (3) it is possible to find coefficients α(i),
a, b, and c and then to define from the expression (1) the depth value in a new grid-point.
Repeating this procedure for all grid-points of the area makes it possible to create the digital gridded
bathymetry with arbitrary spatial grid-steps.
|