|
1.3 ボルトの締付け法
現在船舶用機関の主要ボルトの締付け法として一般に広く行われている方法として
1)伸び計測法(ストレッチ法)
2)トルク法
3)回転角度法
が上げられる。
1)伸び計測法(ストレッチ法)
この方法は基本的に軸力を伸びにおきかえて計測しているために前項で述べたねじ部および座面の摩擦係数に全く関係なく締付力を与えられる点で締付け精度は最も期待できる。この方法の難点は作業能率の点で問題があり、大量生産などの場合不適当である点、また伸びを計測するための測定工具が必要でこれをセットするためのスペースを要する点、計測に或る程度の熟練が必要な点などがこの方法が広く用いられない要因となっている。
また、補・1図(B)のようなヘッドボルトの場合、そのままではこの方法の適用が困難で、これを適用するためにはボルトを中空ボルトにして補・4図のようなデプスゲージを用いるか、またはボルト側にあらかじめピンをセットしたボルトを用いるなどの工夫が必要である。
補・4図
これと同じ思想に基づく締付け法として中大型機関などでボルトの径が大きく充分な締付けトルクを与えることが困難な場合用いられる油圧ジャッキによる方法(補・5図)がある。すなわち、あらかじめ適正締付けに相当する油圧を油圧ジャッキにかけボルトに引張力を与えてボルトが伸びた状態でナットをセットする方法である。
また油圧ジャッキのかわりにボルトをあらかじめ適正締付け状態になる寸法に加熱して熱膨張させた状態でナットをセットする方法などは皆この伸び計測法の分類に入る。この方法はシリンダヘッドの締付け、主軸受冠の締付けなどに主として用いられる。
補・5図
2)トルク法
トルク法はトルクレンチを用いて締付けを行う方法で船舶用機関の締付けに最も多く一般的に用いられる方法である。しかし、このトルク法は前項で述べたようにねじ部および座面の摩擦係数によって締付力が90%近く支配されるという基本的な問題をかかえている。したがってトルク法によって精度の高い締付けを期待することは基本的に無理であるが、少しでも精度を上げるためにはねじ部および座面の加工精度を厳密に管理し、締付けに際して用いる潤滑剤を規定し、同じチャージのボルトについてあらかじめ充分締付けトルクと軸力の関係を把握しておくことが必要である。
3)回転角度法
この方法の欠点はスナッグトルク(肌付トルク)の確定が困難である点である。したがってこの方法で精度の高い締付けを得るためには降伏点を超えた塑性域で締付けを行う必要がある。
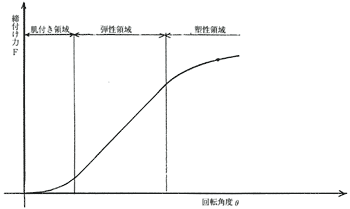
もし弾性領域で締付けを行った場合には締付け精度はトルク法と変わらなくなる。また締付け精度を充分上げるためには補・6図より想定されるように相当深く塑性域に入るように角度を設定する必要がある。しかしこのようにするとボルトの再使用が極めて限られる点、および塑性伸びの限界管理が難しいなどの問題が起こってくる。また、この方法による締付け適用ボルトとしては回転角度が大きくとれる比較的長いボルトまたは細い幹部をもつテンションボルトに限られる点が上げられる。また、この締付け法の場合、接手側のばね常数が回転角度に大きく影響してくる点にも注意すべきである。
このように締付力の精度を上げるためには伸び計測法以外はいずれも難点があり、伸び計測法も適用にはいろいろ問題があるために新しく考え出された方法としてトルク勾配法がある。
補・6図
| (拡大画面:8KB) |
 |
4)トルク勾配法
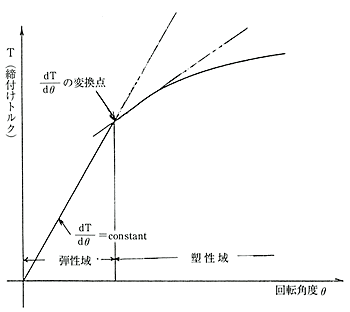
トルク勾配法は一名降伏点締付け法ともいわれ、金属材料が引張力を受けた場合、弾性限を超えると急激に引張力に対して伸びが増大(すなわち降伏)する性質を利用した締付け法である。この方法は既に古くからドイツの自動車用エンジン業界でボルト締付けの信頼性向上に実績を上げている方法で特殊工具を用いボルト締付けの際に感知される締付力と回転角の変化を電気的センサでとらえ降伏点直前で締付けを行う方法である。この場合の締付力のばらつきは同一組立ロット内のボルト材の降伏点のばらつきによって決まる。
補・7図
| (拡大画面:11KB) |
 |
この方法によって締付けられたボルトに外力がかかった場合について検討してみる。
ボルトにトルクを与えて締付けた場合、ボルトには引張力とねじり応力が加わる。
前項で述べたように締付けトルクと軸力の関係は
T=kFdb・・・(1)
で与えられる。
締付けトルクによってボルトにかかるせん断応力は
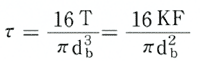 ・・・(2)
一方軸力によってボルトにかかる引張応力は
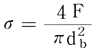 ・・・(3)
ボルトの材質は炭素鋼、合金鋼などの鉄鋼が殆どであるから、この場合せん断ひずみエネルギー説が適用されるのでボルトにかかる応力は
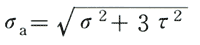 ・・・(4)
降伏点まで締付けた場合は
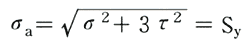 ・・・(5)
したがって単純引張応力より低い値でボルトは降伏する。
(2)(3)式を(5)式に代入すると
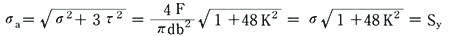 ・・・(6)
となる。したがってこの場合の締付応力は
この状態で外力がかかった場合2つのケースが考えられる。
補・8図
| (拡大画面:35KB) |
 |
第1のケースは締付けを終了した段階で、ボルトのスプリングバックが座面の摩擦係数に打ちかってボルト内部のねじり応力が完全に消失した場合でこの場合、ボルトの降伏点は補・8図のAになりボルトの挙動は全て弾性限内のものとなる。
また、ねじり応力が部分的に残存する場合でも締付部に振動外力がかかると所謂セルフルーズニング現象によってねじり応力は漸次減少し、最終的には完全に消滅するといわれている。したがってこの場合σa=σ=Syとなり、弾性限度迄ボルト側に変動荷重がかけられるとするとボルト側に掛けられる最大許容変動荷重は
となる(ボルト径20mm、ねじ部および座面の摩擦径数をμ=0.15とした場合、K=0.208、σb≒0.43Syとなる。すなわち降伏点応力の43%に相当する外力がかけられることになる。)
第2のケースは、実際にこのようなことは有り得ないが100%ねじり応力が残留したと仮定した場合で、この状態で外力が加わるとボルトは塑性的に伸び、この間の冷間加工硬化によってD点が新しい降伏点となる。そしてボルトの外力が除去されると締付釣合三角形はD点に移動する。この場合、ボルトにかかる繰り返し外力はFb+△Fbとなるが残存締付力Frには変化が生じない。これと同様な仮定に立てば回転角度法によって塑性領域深くボルトが締付けられた場合も繰り返し外力がかかる度にD点が移動し、最終的には弾性域内締付けに落ち着くことになる。ただしこの場合ボルトの永久伸びfzの値が増すだけである。
|