前節の始めに示したモデルに話を戻そう。前節ではこの系においてMを始めに一度引っ張って離す。あるいははじくなどしてこの系を振動状態に入らせた後は外部から全くなにもしない場合、すなわち自然振動状態を考えた。このような条件での振動はすでに述べたようにそのままでは振動系自身の内部摩擦や系の振動が空気をかきまわすなどのために次第に減衰して必ず静止にいたる。その状態の時間経過を示したのが補・37図である。ふつう減衰があっても、この図に示すT'は固有周期T0と余り変わらない。ただし減衰作用が非常に強い場合は当然T'の値とT0とは大きく異なる。しかしふつうに観測される自然振動では周期に相当するT'はT0に等しいと考えて大きな誤りはない。

さて、このkとMの系においてMに対して外部から周期的な強制力を連続して与えた場合を考える。

　

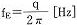
　例えば最も簡単な形の周期 の交番力

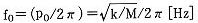
を加えつづけたとする。そうするとこの系は の固有振動ではなく、外からの交番力の振動数に等しい振動

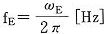
を続ける。この強制力と同じ振動数の の振動を強制振動と呼ぶ。ただし注意しなければならないのはこの場合でも、Eの力を加え始めた当初はこの系には強制振動と一緒に

　x0=A cos(q0^t+ε0)という自然振動が重なって発生する。しかしこの自然振動は初期的なものでしばらくすれば消えてしまい強制振動のみが継続される。

　ただし強制外力が作用し始めた瞬間を含む短い時間内の系の振動とか、強制力がごく短い間だけしか働かずその間の系の挙動を詳細に解析しなければならないなどという場合にはふたつの振動の重なりを考えねばならない。例えば地震により物体が揺すられるような場合、機械を動かし始めた瞬間の機械全体あるいは軸系の振動などを取り扱う場合などがこれに相当する。しかし、我々が機関整備の上で取り扱うことの多いのは定常的に運転を続ける機関の軸系に生じる振動でそれは機関の回転力による強制振動である。強制振動は強制力の振動数qが固有振動数P0に近いかどうかで振動の状態が著しく変化する。強制力の振動数が固有振動に比べて十分小さい場合、すなわち

であれば強制振動の振幅BはB≒E/kとなる。すなわち強制力の振幅に等しい一定の力Eでばねkを引っ張った時の伸び(E/k)に等しい振幅で振動する。これに対し、強制力の振動数が固有振動数に比べて遥かに大きい場合にはその振幅はB≒Oとなる

　すなわちほとんど振動しなくなる。問題なのはq≒P0の場合の状態である。この状態での系の挙動は先に述べた振動系に働くあるいは内在する減衰作用の大小に強く影響される。減衰の作用が小さい系ではq=pにおいて振幅Bは非常に大きくなる。すなわちよく知られた共振状態(Resonance)が出現する。その条件は実際上はB=∞となり、この例のようなばねならばその弾性限界を超えるような大振幅が発生し、ばねの破断などの系の構造が破壊されることになる。また十分大きな減衰要素が系に含まれる場合にはf=f0の近くでの共振現象を抑え　までにすることができる。要するにf≒f0での強制振動の振幅は系の減衰要素の強弱次第で定まるということである。したがって問題にしている系がq≒p0の強制力を受けざるを得ない場合、その強制力による強制振動の振幅をなるべく小さくするためには系に内在する摩擦による減衰効果が期待できないときには必要なだけの減衰作用を与えることができる装置、すなわち適当なダンパのようなものを特別に系に取り付けなければならないことになる。

　以上はごく単純な系について強制振動の説明をしたが、ここでわれわれが取り扱うとしている機関のねじり振動系でもこれと全く同じ現象が生じる。機関の運転中にはクランク軸にはプロペラをまわすための大きなトルクをピストンからコンロッドを介して受ける。もちろんクランク軸、プロペラ軸はいずれもこの大きな推進トルクに耐えるだけの十分なねじり剛性をもっている。問題は機関から与えられる回転力(トルク)は時間的に一定したものでなく、クランク角の位置に応じて変動する成分を含むことである。すなわちその変動成分が機関のクランク軸系に強制振動を発生させることである。もちろん上に述べたようにクランク軸系は十分なねじり剛さをもっているから、変動する変動回転力成分とクランク軸系の固有振動とが共振状態を生じない限り強度上の不安はない。しかし、クランク軸系は先に述べたように多数の固有振動をもっている。したがって機関の回転力の変動部分は機関の使用回転、速度範囲でいくつかの固有振動と共振状態になる可能性が必ずあるということである。さらにさらに厄介なのはこの回転力の変動成分は簡単なものでないという点である。

　その変動成分の発生はまず、ピストンを動かしているのが燃焼ガスの圧力であり、当然空気の吸入燃焼という燃焼サイクルに応じた息付きをしながらクランクをまわしていることによる。次に大きな質量をもったピストン、コンロッドがピストンクランク機構という複雑なメカニズムを介してガス圧力をトルクに変換するという機構学的必然もその原因となる。要するにピストンクランク機構により燃焼ガス圧力から回転力を取り出す過程では必ずクランク角によって変化する成分を含むことである。このことはわれわれが自転車を漕ぐ場合に体感できることである。回転力の変動についてもう少し詳細に述べることにする。

　いま考えている機関を4ストロークサイクルでZ個のシリンダ数のものであるとする。この機関がn rpmで定常運転しているとする。各シリンダは2回転に1回、等間隔に燃焼する。それら各シリンダにおける燃焼状態が完全に同一であるとする。この機関の1個当たりのシリンダから燃焼ガスより発生する回転力NE(t)は、上に述べたように4ストロークサイクルであるから機関が2回転するのに必要な時間TEを周期とする周期関数である。そのことからフーリエ(Fourier)の定理に基づき、

　ただし

となる。

　要するにシリンダ当たりの回転力NE(t)は一定回転力N0と基本周波数fe＝qe/(4π)(1/2)×(n/60)[Hz]のフーリエ級数すなわち、式(11)のようなfe、2fe、3fe……という周期のcosine形の変動成分の和となる。これらの変動成分はこのようにfeの整数倍の振動数を持つわけであるが、この場合に限り毎秒当たりの回転数を基準にして1/2次、1次、r/2次と呼ぶ。

　プロペラに伝えられて推進に寄与するのはこの定数2項成分N0であり、Z個のシリンダを持つこの機関ではZ・N0の回転力がプロペラを介して有効な推進仕事をする。クランク軸、中間軸、プロペラ軸は当然この回転力N0に応じた量だけねじれる。しかしそのねじれ角は大きいが一定しており時間的に変動はしない。このねじれは始めに述べた例において重りを吊した時のΔLに相当する量である。N0以外の成分、すなわちN(1/2)cos(1/2qet+α1/2)、N1cos(qet+α1)、N3/2cos(3/2・qet+α3/2)、……が軸にそれぞれの振動数qe/2、qe、3/2qe……の振動数の強制振動を誘起する。そしてそれぞれの強制振動のねじれ角がz・N0による定常ねじれ角に重なってクランク軸、中間軸、プロペラ軸などに生じる。しかし先に述べたように軸系の固有振動と共鳴状態に入らない限り、そのねじれ角は問題にならない。すなわち(s/2)次の回転力成分と軸系のr節の共振状態すなわち

となる回転速度について詳細に検討すればよい。この速度を危険速度と呼ぶ。先に述べたように軸系の固有振動はいくつも存在するが問題になるのは比較的低い節数のもので、通常の中速機関では1節と2節を考慮すればよい。　高速機関の場合は4節、5節に対する危険速度が問題になることがある。軸系の固有振動数fuが判っていれば上の式(12)からr節(s/2)次の共振に対応する危険速度ncは

と簡単に求まる。重要なのはこの危険速度におけるねじれ振動の振幅値である。それを求めるためにはまずこの危険速度の振動に対応する減衰効果である。これに対しては実用に供せられるような理論値は全くなく、適当な理論に経験による数値を与えて振幅計算を行う。さらにこの計算を行う場合にはN0の場合と同様シリンダ数がZ個あることを考慮せねばならない。N0の場合は単純にzN0とできたが変動成分はこれほど簡単にいかない。Z個のシリンダの効果はシリンダの点火順序に基づく各シリンダの回転力成分間の位相差ならびに問題としている固有振動のモードを考慮に入れたちょっと面倒なベクトル計算を行わなねばならない。こういう計算を行うとsの値がzの整数倍となる回転成分との共振が大きな振幅を生じ易いことが判る。この場合を大危険速度Major Critical Speed、それ以外を小危険速度Minor Critical Speedという。

　このようにして、それぞれの機関について具体的に危険速度ならびにそのときのねじり振動の振幅が計算される。その1例を補・38図に示す。これは補・36図に相当軸系を示した舶用機関軸系であり、その軸系における機関の第1シリンダ位置でのねじれ振動の角振幅がそれぞれの危険速度に対応して示されている。機関軸のこの位置での振幅が判ればそのときのこの軸系の各慣性モーメントすなわちJ1、J2、……間のねじれ振幅並びにそのねじれに基因するトルクがホルツァの表から計算できる。トルクが判ればねじれによるせん断応力を算定することができ、そのせん断応力値、すなわちせん断応力振幅が疲労破壊に対する許容値以下であるかどうかが判断出来ることになる。もしねじれ振動による応力振幅が許容値を越す場合はその危険速度の付近での連続運転は避けねばならない。また適当なダンパ(Dumper)をつけて振幅を抑えることが行われる。その場合はダンパをつけた状態での振動計算がなされる。

　

　一般に新造船の機関軸系はもちろん、機関軸系を変更した場合には必ずその軸系についてねじり振動の計算が行われ、その結果が提示されると同時に運転時にねじり振動が実測され、計算結果との照合が行われる。どのような現象でも実測に勝る検証はないのであるが、一般に実測を正しく行うことは易しいことではない。現在では優秀なねじり振動計が国内でも製造されており、これらを正しく使用すれば十分に正確なねじり振動の振幅を知ることができる。しかし一般にその測定位置は機関自由端であり、軸系上の任意の点、あるいは危険断面でのねじり角振幅を知るには実測値に基づきホルツア表から計算して求めねばならない。したがって機関軸系の安全運転のためにはその軸系の固有振動を求めたホルツア表がどうしても必要である。そしてこれを十分使いこなすように心掛ける必要がある。また、振動計を用いてまず計測されるのは軸系に生じている種々な振動の重なりあったものである。これを周波数分析装置を用いて個々の振動成分に分けた後、問題としているねじり振動成分を摘出して観測するわけである。現在ではこの過程も非常に簡単に行えるように機器が発達しているが、それだけに現象の本質を見誤らないようにすることが必要である。ねじり振動はもし問題になるような場合はクランク軸の折損というような深刻な事態につながるので特に注意を要する。

　

　最近になり、舶用機関に高速機関が広く用いられ始めている。それに伴い、機関につながる軸系の回転数も次第に高速化して来た。同じ動力を伝える場合、回転数が高ければそれに逆比例して伝達回転力は小さくなり、したがって軸はそれだけ細くなる。この様な場合に考慮しなければならない現象が最近舶用の軸系でも問題になって来ている。この現象について述べよう。

　補・39図に示すように比較的細い一様な軸の中央に質量Mの円板が乗っている。このMをハンマで叩いたとするとこの系はMを集中荷重、軸の曲げ剛性を復元力とする横振動をすることはすぐに想像できる。ただ一般にこの振動は振動数が高く、直接目で見ることは難しい。しかし軸にストレンゲージを貼りつけて観測すれば簡単にオシログラフの画面で振動を見ることができる。この図のような単純な軸系であればその固有振動数は簡単に

ともとまる。KLは材料力学でよく知られているビームの式から

と求めることが出来る。ただし、Eは鋼の縦弾性係数、Iは軸の断面2次モーメントである。今この軸をnc≡60fL[min^-1]で回転させるとすると軸はすさまじいふれまわりを始め、たちまち大きく曲がり、破壊する。そこでここで定義した横振動数に対応する回転数nc[min^-1]をふれまわりの危険速度Critical Speedという。実際問題として軸はn=0.8nc[min^-1]でもふれまわりが激しく、とても定常的な運転をすることはできない。したがって機械は軸系の回転速度n[min^-1]が

の範囲では連続運転をしない事になっている。

　舶用の機関の場合、主軸系のフランジを現場や工場で不用意に重いものに変えたり、またねじり強度の上からは十分の強さがあるからという理由で主軸系の一部や機関付属の機器類の軸を細くするなどのことを行うと、この危険速度の影響でふれまわりが大きくなる場合を生じる。横振動も正確にいえばどの軸系もいくつかの固有振動数が存在するから当然それぞれに対応する危険速度が存在する。しかし多くの場合は最も低い横振動数に対応する危険速度のみが問題となる。この現象で注意しなければならないのは、この現象は力学的不安定現象であり、振動に減衰を与えれば防止できるとか、危険速度でのふれまわりを小さくおさえることは本質的に不可能である。軸にのっている、質量を減ずる、ベアリング間隔を短くする、軸の曲げ剛性を大きくする、すなわち軸を太くするなどの系の振動特性を代えてfLの値、したがってncの値を変更する以外にこの現象から逃れる方法はないことである。

　なお、数値例として、l=1、800mm、M=5.0kg、軸径d=30mmの場合を考えると、I=3.97×10⁴mm⁴となるから、E=2.06×10⁵N/mm²を用いると、K:67.4N/mmであり、p=116　1/s　すなわちnc=1109rpmとなる。