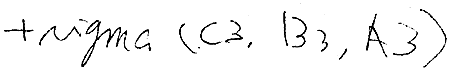3. Specific Volume Anomaly and Density Anomaly of Seawater
The international equation of state for seawater diluted with pure water or concentrated by evaporation has been determined to be used with the practical salinity scale (Millero et al., 1980; Millero and Poisson, 1981). This equation is more precise than the currently used equations (Knudsen et al., 1902; Ekman, 1908; Cox et al., 1970) and covers a wider range of temperature and pressure. Data reports describing the details of the fitting procedure are available (Millero, Chen, Bradshaw and Schleicher, Unesco Report No. 38 (1981); Millero and Poisson, Unesco Report No. 38 (1981).

p (S, t, p) = p (S, t, 0)/[1-p/k (S, t, p)] (7)
where K (S, t, p) is the secant bulk modulus. The specific volume (V = 1/pm3/kg) of seawater can be obtained from
V (S, t, p) = V (S, t, 0). [1-p/K (S, t, p)] (8)
Because the maximum variation of density and specific volume of sea water is less than 7 percent over the oceanic range of variables, numerical precision is lost by retaining the full numerical magnitude. A 32 bit single precision floating point number has about 7 significant decimal digits. While such precision exceeds the accuracy of the measurements and is adequate for most purposes where the full value is required, it is insufficient for taking differences for Brunt-Vaisala frequency calculations. An improvement by two orders of magnitude in the oceanographic range is obtained by computing specific volume anomaly δ defined by:
δ = V (S, t, p) - V (35, 0, p) (9)
and reported in units of 10-8m3/kg.
For many oceanographic applications, the specific volume (or steric) anomaly δ provides a more convenient measure of the baroclinic structure in the ocean. For computational convenience, V(35, 0, p) bas been obtained from the EOS80 by evaluating the coefficients for a salinity of 35 (PSS-78) and temperature of 0℃ (IPTS-68) in the form
V (35, 0, p) = V (35, 0, 0)・[1 - p/K(35, 0, p)] (10)
K (35, 0, p) = K0 + A0p + B0p2