ここで、eは乱流エネルギー密度、Lは混合距離に相当する乱流の散逸度、そしてmはパラメータ。ここでは、混合距離Lは境界層理論に基づく経験的な双曲線応答式、eについては輸送方程式から決定するという1方程式乱流モデルの方法を選んだ。

最後に塩分と温度については、海底で拡散フラックスをともにゼロ、海面では塩素量のみ拡散フラックスをゼロとするが、温度については接水気層との熱交換を次式で計算し、表層への受熱フラックスとした;

Q=Q_s-Q_b-Q_h-Q_e

ここで、Qは海面を通じての正味の受熱量、Q_bは海表面からの逆輻射量、Q_hは顕熱量(対流により大気と海面の間を出入りする熱交換量)、Q_bは潜熱量(蒸発・凝縮による熱移動量)を表わし、気象要素からそれぞれ次のように求められる。

　

［吸収日射量］

Q_s=(1-γ)[1-(1-K)n]×Q_s0

ここで、Q_s0は完全晴天時の海面日射量、γは海面の反射率、nは0.1単位の雲量、Kは太陽高度。

　

［有効逆放射量］

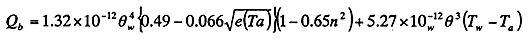
ここで、Twは水温(℃)、T_aは接水気温(℃)、θ_w=273+T_wは絶対温度(K)、e(T_a=f・e_s(T_a)は大気の蒸気圧(hPa)、fは相対湿度、e_s(T_a)は温度T_aにおける飽和蒸気圧(hPa)、nは0.1単位の雲量。飽和蒸気圧e_s(T_a)の計算はGolf-Gratch式による。

　

［乱流熱伝達量］

Q_c=K_c(T_w-T_a)

K_cは乱流熱伝達量係数で、経験的に海上風速W(m/s)に比例するとして、

K_c=2.77×10^-4(0.48+0.272W)　(cal・cm^-2・S^-1・℃^-1)

前ページ　　　目次へ　　　次ページ