近距離伝搬の方程式は、次の(6・4)式となる。

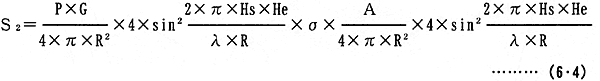
こゝでHsはレーダーアンテナの海面上の高さで、Heは物標の海面上の高さで、λはレーダー電波の波長である。(6・4)式に4×sin²{2×π×Hs×He/(λ×R)}が入っているのはレーダーから物標までの直接波と海面で反射してくる間接波との電波伝搬経路差による位相差を考えたベクトル的合成電力を考えるからである(付録1参照)。

次に、(6・4)式を整理すると、(6・5)式のようになる。

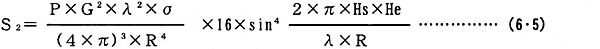
sin{(2×π×Hs×He)/(λ×R)}は0〜1の値をとるので、S₂の値は(6・3)式の値(距離の4乗に逆比例)に沿いながら、距離Rが遠くなるに従い最大(16倍)と最小(0)を示しつゝ、sin⁴の曲線に従って次第に減少することゝなる。

　

6・3・1・3　海上の遠距離におけるレーダー電波伝搬方程式

前述のように、海面が地球表面に沿って湾曲していることを考慮しなければならないような遠距離の伝搬の場合は、図6・6のように、海面上の反射点における水平線を引いて考え、レーダー・アンテナ及び物標の高さのうち、その水平線より上の部分をそれぞれAs及びAeとする。そして、(6・5)式のHs、Heの代りにAs、Aeを入れれば、(6・6)式が成り立つ。

前ページ　　　目次へ　　　次ページ