Fig. 3 Predicted and measured dew points

Table 2 Test condition

　

3.2　HEAT TRANSFER CALCULATION OF FIN

The inner wall temperature of the polycarbonate test section was 85℃ as a maximum, The contribution ratio of the radiation heat flux from the inner wall to the test tubes was within 5%, of the total heat flux q_T When the emissivity of the polycarbonatc wall and the tubes covered with the condensate were assumed as 1 . As an accurate estimation of the radiation heat transfer is difficult, it was neglected in the following analysis. The total heat flux q_T consists of the convection heat flux q_V and the condensation heat flux q_C as

q_W = (q_V + q_C)(AB + A_Fη)/A_W　(8)

where A_W is defined as the heat transfer area when the fin height is 0. In the experiments, q_W was obtained from the temperature difference and flow rate of the cooling water. The convection heat flux is expressed as

q_V = h_V (T_f - T_W)　(9)

The condensation heat flux q_C can be expressed as,

q_C = h_CL_W(C_f - C_W)　(10)

The following empirical correlation [4] was available in the range of 2 × 10³ ＜ Re_f ≦ 5 × 10⁵

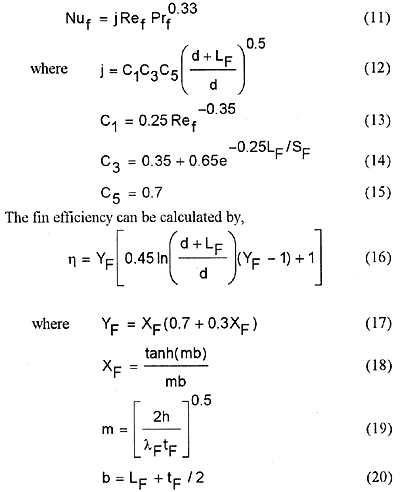
The fin efficiency strongly depends on the heat transfer coefficient, h, in Eq.(19). These correlations were obtained from the single-phase experiment where the heat flux is a simple multiple of the constant heat transfer coefficient and the temperature difference between wall and fluid. Although the condensation heat flux can not be expressed with the above simple relation, it is considered that the Eq.(19) with the larger heat transfer coefficient taking account of the condensation heat transfer would give an approximation. As a first attempt. the following equivalent heat transfer coefficient in the condensation region was used.

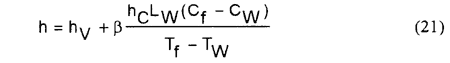
wher β=1 for the usual calculation.

　

Fig. 4　Approximation of heat flux distribution

BACK　　　CONTENTS　　　NEXT