For the first time, these models were proposed by Kawasaki [4] about twenty years ago. In particular assuming that all the distribution controlling the time from good condition to defect occurrence, the time from defect occurrence to failure and so on are exponential, we investigated the characteristics of the maintenance method using the diagnosis success ratio. As the results, we make it clear that PM and CM depend on the diagnosis success ratio only whether the diagnosis takes time or not [2].

Here using the fault diagnosis success ratio, we study on some methods for evaluating maintenance from the standpoint of the cost and the number of PM and CM, and improvement ratio of reliability. Besides, we also assume that all the distribution is exponential one.

　

Figure 1. Process of failure occurrence through defect.

　

2. THEORETICAL BACKGROUND

　

First we summarize the necessary symbols and terms for studying here. As already described, assume that all the distribution are exponential.

　

2.1 Symbol

F(t), f(t): Failure distribution function and its pdf (probability density function)

F_d(t), f_d(t): Distribution function of time from normal to defect and its pdf

F_e(t), f_e(t): Distribution function of time from defect to failure and its pdf

F_m(t),f_m(t): Distribution function of necessary time for diagnosis and its pdf

p: Diagnosis success ratio (O≦p≦1)

T_d: Mean time from normal to defect (In case of exponential T_dd = 1/λ_d)

T_e: Mean time from defect to failure (In case of exponential T_e = 1/λ_e)

T_m: Mean time for diagnosis (In case of exponential T_dd = 1/λ_d)

T: MTBF of the basic model from normal to failure

T_vi: Mean time of interval of CM (i = a, b)

T_wi: Mean time of PM (i = a, b)

Besides, i = a, b shows Model A and Model B respectively.

　

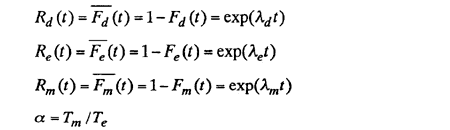
2.2 Diagnosis success ratio: p

The distribution of diagnosis time t_m is F_m(t), and the time from defect to failure is t_e, and its pdf is f_e (t). The diagnosis success ratio is the case of t_m < t_e, that is, before occurring failure, the dragnosis must be finished [5]. Therefore, we can provide the definition of the diagnosis success ratio.

　

　

Example.1 The diagnosis success ratio p in case of exponential distribution

In this case, from Symbols and terms, we can easily obtain the following relations:

F_e(t) = λ_e exp(-λ_et) and F_m(t) = 1 - exp(-λ_mt)

and then substituting them into eq.(1), the success ratio can be obtained as

BACK　　　CONTENTS　　　NEXT