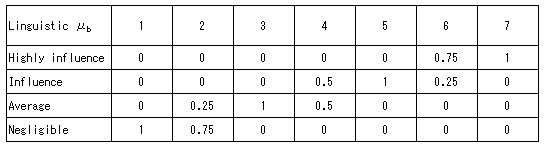
Table 7 Membership values of influenced degree

　

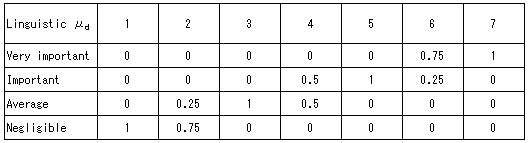
As mentioned above, the important degree is a result considering necessary, failure degree, influence degree and influenced degree, alternative set (or defined importance degree set) can be represented with μ_d and as shown in Table 8:

　

Table 8 Membership values of important degree

　

In this research the factors affecting importance degree include necessary, failure degree, influence degree and influenced degree. The different weight must be given because each factor has a different function in calculation. To determine the weight of factor the comparison method in twos is used [2]. Suppose that factor set may be represented with μ_a= (μ_a1,μ_a2…μ_ai…, μ_aj,…,μ_an), μ_ai,j is used to represent the result of comparing μ_ai and μ_aj in twos, i.e

　

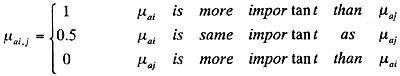
Table 9 The calculated result of factores

　

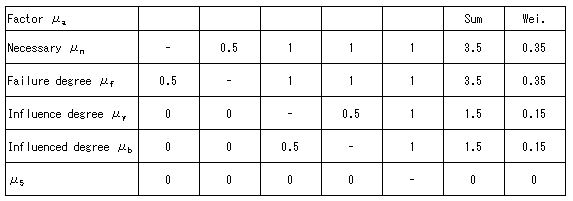
An assumed factor μ_an+1 is used to prevent the werght of factor being zero, this assumed factor being the most valueless in all factors. It can be represented with μ₅.

　

Factor set can be as shown in Table 9 :

The Assessed result μ_c can be got = factor set ・ assessment matrix = μ_a ・μ_r

Based on the character, failure information and influence factor of module, each assessed result of module can be got μ_ci = μ_ai ・μ_ri.

It may be known that module belongs to which important degree after the result is compares with alternative set μ_d.

Because the assessed result is not right equal to the value of alternative set the best-fit method may be used to resolve this problem.

　

3. THE DETERMINATION OF IMPORTANCE DEGREE OF MODULE

　

The method uses distance between μ_ci and each of the importance degree expression to represent the degree to which μ_ci is belong to each of them. The distance can be defined as follows [1,2]:

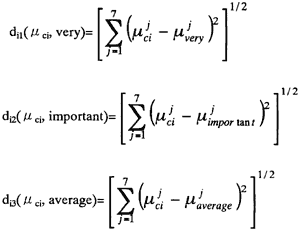
BACK　　　CONTENTS　　　NEXT