Probability distributions and detailed data are used to describe and deal with the importance degree of equipment. However in many cases it may be difficult to precisely determine the parameters of probability distributions and detailed data due to lack of evidence, specially in modular design because each module consists of many equipment, pipes, and valves etc. Therefore fuzzy function is attempted to use to resolve this problem.

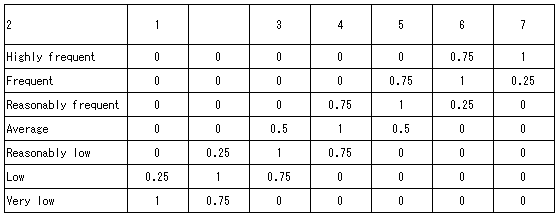
In fuzzy theory, linguistic variables can be characterized by their membership functions to a set of categories which describe the degrees of property about ship. For instance, if U=(1,2,3,…,n-1,n) represent a set of categories, the linguistic variables 'very good', 'good', 'average' and 'poor' may be modeled by[1,2]:

'very good' ={0/1,…,0/n-3,0/n-2,0.75/n-1,1.0/n}

'good' ={0 11,…,0.5/n-3,1/n-2,0.25/n-1,0/n}

'average' ={0/1,0.25/2, 1/3,…,0/n-2,0/n-1,0/n}

'poor' ={1.0/1,0.75/2,0/3,…,0/n-2,0/n-3,0/n}

Where the integers in the numerators of each term within the brackets represent the categories and the real numbers in the denominators stand for the membership degrees.

The membership values for the components in U belonging to each of the linguistic variables 'very good', 'good', 'average' and 'poor' can be denoted as follows in Table 1 if n=7:

Table 1 Membership values of U

　

Therefore we can get the linguistic variable of factor affecting importance degree.

The necessity can be defined as the necessary degree of module in system, i.e. which role is played in system. It can be represented withμ_n and as shown in Table 2:

　

Table 2 Membership values of necessary degree

Table 3 Membership values of failure likelihood

　

In the past the failure rate is only considered in engineering calculation. Actually there are other factors must be considered, here a new concept of failure degree is introduced. The failure degree can be defined as a result considered the failure likelihood, consequence severity and failure consequence probability. It can be represented withμ_f.

Failure likelihood can be defined as the failure occurrence likelihood of each module of system. It can be represented withμ_l and as shown in Table 3:

Failure consequence severity can be defined the severity of resulting effects. It can be represented withμ_sand as shown in Table 4:

Table 4 Membership values of failure consequence severity

　

Consequence severity probability can be defined as the likelihood that the failure effect of the identified failure will occur. It can be represented withμ_p and as shown in Table 5 :

　

Table 5 Membership values of consequence severity probability

　

Failure degree (μ_f) can be got with consequence severity O (failure consequence probability×failure likelihood):

　

μ_f=μ_sO(μ_p×μ_l)

　

The influence degree can be defined as the degree to influence other module. It can be represented with μ_y and as shown in Table 6:

　

Table 6 Membership values of influence degree

　

The influenced degree can be defined as the degree influenced by other module. It can be represented withμ_b and as shown in Table 7:

BACK　　　CONTENTS　　　NEXT