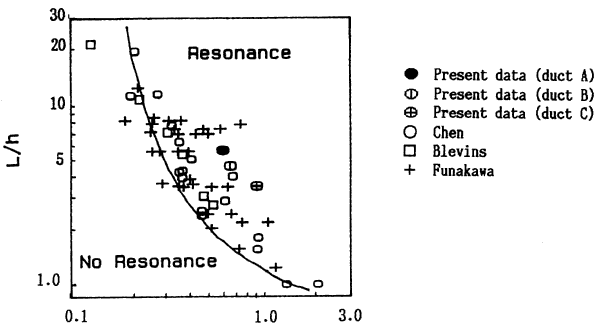
Fig. 8 Resonance Parameter for Tube Arrays

　

On the other hand, the data points by Chen [7], Blevins [4] and Funakawa [8] are described in Fig. 8. It should be noted that the critical Reynolds number in the parameter (G_s) is based on the flow velocity in the gap between tubes in the same row. This is so even when this velocity is not the highest one within the array.

Although the resonance parameter (G_s) correlates the experimental data points relatively well, further research is required and further refinement of G_s may be necessary. This is because all the data, points used are from laboratory tests; no industrial data points are available. The resonance parameter (G_s) does not apply to very large spacing, i.e. X_L > 6. This range of tube spacings has very little value, if any at all, for practical applications.

The procedure of predicting and suppressing the occurrence of acoustical resonances in heat exchanger units consists of three steps, each of which is outlined here only briefly.

Step 1: Estimation of the frequencies

The frequencies of the acoustical modes of the tube array container (f_n where n = 1, 2, 3) are estimated from the equations:

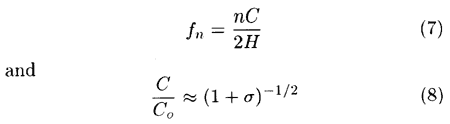
where H is the container dimension in the direction normal to the flow and the tube axes. C is the effective speed of sound. C_o is the speed of sound, σ is the solidity ratio and n is the mode order (i.e. number of the acoustical half waves along the dimension H). If the container is not fully filled with the tubes, an estimate of C/C_o can be obtained from the data given in section.

Step 2: Estimation of the critical velocities

The critical flow velocities, (V_cr)_n, at which the frequency coincidence occurs are determined from the relation:

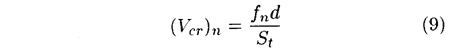
where, d is the tube diameter and S_t is the Strouhal number which depends on the tube spacing ratios, X_L and X_T. Charts of Strouhal numbers can be found in Reference [3].

Step 3: Estimation of the resonance parameter

When several (or only one) of the critical flow velocities are found to be lower than 120 % of the maxmum velocity of the unit operation, the resonance parameter (G_s) must be calculated for the highest, (V_cr)_n. If the value of the resonance parameter lies in the non resonant region, resonance will not occur at any of these critical flow velocities and, therefore, antiresonance counter-measures are not needed. When the value of the resonance parameter is in the resonant region, resonance will occur at (V_cr)_n.

　

4. CONCLUSIONS

　

The occurrence of acoustical resonance in a staggered array of closely packed rigid tubes has been investigated by means of wind tunnel tests. The test results lead to the following conclusions.

1. This investigation has clearly shown that the frequency of vortex shedding does not coincide with the acoustical frequency at onset of resonance.

2. The acoustical Strouhal number bears no simple relationship to the vortex shedding Strouhal number.

3. Tightly spaced tube bundles are generally quieter than more widely spaced tube bundles.

BACK　　　CONTENTS　　　NEXT