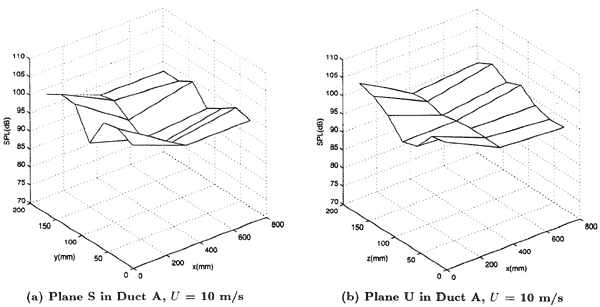
Fig. 7 Sound Pressure Fields over Plane at an Acoustical Mode Frequency of 125 Hz
First, the acoustical natural frequencies (fa) of the transverse modes of the heat exchanger cavity are predicted. Second, the dominant excitation frequency (fs) is predicted, using equation (1), and compared with the acoustical frequency. An acoustical resonance is predicted if fa = fs.
In many cases an acoustical resonance is predicted at, fa = fs, but a loud or damaging resonance does not occur. Grotz and Arnold [5] attributed the absence of a predicted resonance in closely spaced tube bundles to damping of the transverse acoustical wave by the tubes. These methods agree that (1) widely spaced arrays resonate, and (2) closely longitudinal spacing hinders resonance, but none of these methods gives a reliable prediction of the presence or absence of resonance in marginally resonant or closely spaced tube arrays.
Rae and Murry [6] provided an alternative model which explains this phenomenon in terms of a positive feedback mechanism between the fluctuating flow and the acoustical system. The criteria presented by Grotz and Alnold defines a excitation force which will lock on and excite the acoustical ica, mode only when the two frequencies are close to one another. Clearly this investigation has shown that the observed phenomenon does not behave in a manner consistent with this type of excitation mechanism.
Ziada and Oengoren [3] pinpoint several parameters which should be considered when evaluating acoustical resonances in tube arrays. The first parameter is the critical Reynolds number (Rcr), based on the critical gap velocity (Vcr)' the tube diameter (d) and the kinematic viscosity (v).
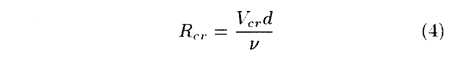
It represents the level of the fluctuating energy associated with the flow periodicity when the frequency matching occurs.
The second parameter is the spacing ratios. XL and XT. They determine: the range of Reynolds number at which this excitation is active; the resistance to the acoustical wave propagation between the tubes and the Strouhal number of the flow excitation.
The last parameter is a scaling parameter. A dimensionless parameter which contains all the variables that need scaling is the acoustical Reynolds number,
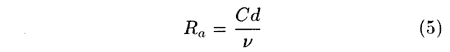
The geometric scaling is taken care of by the tube diameter, whereas the gas properties are scaled by using the effective speed of sound (C), and the kinematic viscosity (v).
In the case of staggered tube arrays, the resonance parameter has the form,
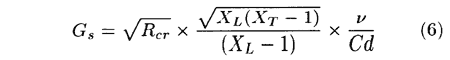
This function is used to correlate the data points with L/h in Fig. 8. The parameter L/h represents the ratio between the length of the flow winding around the tube (L) and the minimum thickness of this flow (h). As shown in Fig. 1,
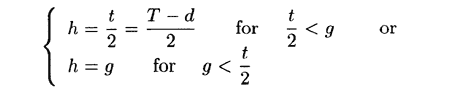
where t is the transverse gap between tubes and g is the minimum gap between tubes. The larger the ratio L/h, the more unstable the flow is and therefore, the more liable the system is to resonance. This behavior is clearly depicted in Fig. 8.
BACK CONTENTS NEXT