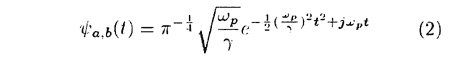
where ωp and γ are, respectively, a center frequency and a parameter that determines the extent of frequency localization.
While the conventional research on WT has focused on the selection of AW's derived from mathematical approaches, measured signals are applied to the AW in this study. As AW's must be localized in both time and frequency domains, the following calculations are made for the sampled signal.
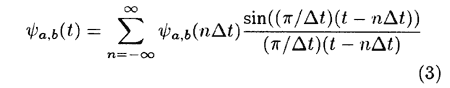
where Δt : time Interval of sampling and ψa,b(nΔt) is a discrete function of AW which is obtained by a measured signal, f(t), When a window signal is dilated or contracted in a form of 2a where "a" is an integer, the results can be derived by ordinary Interpolation or decimation.
As the traditional calculation of correlation repeats the averaging procedure, the original signal must be stationary. To apply the method to time-varying signals, a new concept of instantaneous correlation factor, ICF, is introduced. The ICF is de-noted by the inner product of f(t) multiplied by the complex conjugate of AW, ψ*a,b(t), as shown in Eq.
(4). The calculation coincides with the concept of WT.
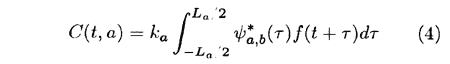
where La is window length, ka is a constant and ka depends on the window length. When f (t) in Eq. (4) is equal to g (t), from which ψa,b (t) is partially taken, an auto-correlation factor is obtained.
Applying the proposed method, the correlations between acoustic signals and vibration signals from a wall and a floor in a mess hall, are analyzed.
3. Simulation: Analysis of simulated signals
A chirp signal, shown In Fig. 1, is analyzed by this method. The result is represented on a semi-log plot of Fig. 2, in which the horizontal axis is time in ms and the vertical axis is scale "a" in the logarithmic value of 2a. The original AW of a = 0 is taken at the center of the signal, that is, t = 80ms, and its window-length is about a half period of the signal. The maximum value of C (t, a) which is equal to 1, is given at the mid-point of distribution, that is, (80ms, 0). At both ends in the direction of the time, distributions of C (t, a) are shifted from a = 0 to a <0 in the direction of the vertical axis. As the mutual-similarity is estimated on the time axis away from t = 80ms, it is proved that the similarity can be obtained from this method and that the variation of harmonics can be analyzed at the transient of the "signal with harmonics*'. It is also confirmed that the mutual-similarities are effectively obtained for many other simulated harmonic signal from this method [6].
On the other hand, Fig. 3 shows an analytical result of a simulated harmonic signal, which includes components of (100 x 2-3) Hz, (100 x 2-1) Hz, (100 x 21) Hz, (100 x 23) Hz. This result is analyzed by AW ψa,b(t), which consist of a 100Hz, sinusoldal conponent . The signal enables us to detect the energy distribution of C (t, -3), C (t, -1), C (t, 1) and C (t, 3). The time resolution becomes more accurate at small scale, while the scale resolution becomes more accurate at large scale. From this figure, it is also confirmed that the mutural-simularities are effectively obtained for the harmonic signals.
Fig. 1 Chirp signal.
Fig. 2 Modified WT, C (t, a), analysis by a measured AW.
Fig. 3 Harmonic signal analysis by C (t, a).