TS-94
Wavelet Transform of the Correlation of Time-varying Signal and its Application to Acoustic Analysis of a Training Ship
Shunsuke ISHIMITSU*, Hajime KITAGAWA** and Satoshi HORIHATA**
ABSTRACT
Recently, many researches on time-frequency analysis using wavelet transform have been focused on analyzing wavelets that are derived from a mathematical approach. In the analysis of this study, measured signal is adopted as the wavelet. Applying the proposed system, the correlation between acoustic and vibration signals from a wall and a floor in a mess hall, which is adjacent to an engine room of the training ship, is analyzed. As the traditional calculation of correlation repeats averaging procedure, the original signal must be stationary. To apply the method to time-varying signals, a new concept of instantaneous correlation factor, ICF, is introduced. As a conclusion, it is proved that a dominant feature of the correlation can be estimated by the ICF. The time-varying correlation could be analyzed and the starting point of main engine deceleration can be detected accurately. We also confirmed that this method allows for selection of reference signals to meet the active control.
Key Words: Wavelet Transform, Analyzing Wavelet, Time-Frequency Analysis, Correlation Ship's Interior Noise.
1. Introduction
Generally, a stationary signal of sound is analyzed either in a time domain or in a frequency domain. A non-stationary signal, on the other hand, must be represented simultaneously in a two-dimensional time-frequency plane, because frequencies of this type of signal evolve in time. Representative time-frequency (t-f) analyses include Spectrogram, Wigner Distribution (WD) [1] and Wavelet Transform (WT) [2]. Spectrogram is hitherto applied to the non-stationary signal analysis. Spectrogram is a very convenient analysis. However, the accuracy of it is not satisfactory and a trade-off exists between in the time domain resolution and in the frequency domain resolution. Recently, both WT and WD have been investigated instead of Spectrogram. While in the calculation of Spectrogram a time window of constant length is applied to the whole frequency range, a frequency-varying window is used in WT. As the window of WT, that is, basic-functions, called analyzing wavelets (AW) are derived from one elementary function by translations and dilations. The multi-resolution analysis enables WT to cover a wide frequency range [3].
Previously, we proposed a correlation function that made use of the WD of each signal and analyzed instantaneous coherence [4]. In the method presented here, correlations between two signals can be immediately obtained by applying measured signals to the AW. As no calculation of the time average is required in this method, the instantaneous correlation is applicable to transient signal analyses.
In this study, vibration signals both from a wall and from a floor in a mess hall of a training ship, the Oshima Maru, are used as the AW. The effects of vlbration on the structure-borne sounds in the room can be represented quantitatively by the WT. In addition, the result applied to the selection of a reference signal for active noise control (ANC) is discussed.
2. Application of measured signal to AW
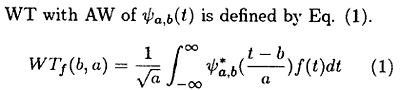
where a, b are scale and shift parameters, respectively, which dilate and translate the AW. The time resolution becomes more accurate at high frequencies, while the frequency resolution becomes more accurate at low frequencies.
Frequently, the Gabor function of Eq. (2) has been applied for the AW because it gives a satisfactory trade-off between time and frequency resolutions.