Fig. 9 Unstable area obtained by steady oil whirl
Fig. 10 Change of unstable area by damping
In this paper, the factors which give the influences to the stable criterion are considered.
It is the self-exciting vibration of the bearing to give the influence to the unstable coupled vibration. Therefore, if the complicated coupled vibration can ultimately come to the single plane motion of the journal by substituting the spring constant of the shaft connecting other related shafts with the equivalent spring constant of the plain motion, then the problem of solving the complicated coupled vibration is changed to the simple problem of determining the conditions to continue the steady oil whirl. This results in the clear elucidation of the phenomena and also gives the simplification of the unstable criterion.
By the assumption of the steady oil whirl, the term of the change of velocity of eccentricity ratio in Eq. (1) can be deleted, the shaft can be considered to vibrate synchronously and steadily with the same frequency and also the spring constant of the shaft can be replaced with the equivalent spring constant in plain motion. Consequently, it is possible to simplify the said model intensively to the single plain motion. Hence by representing the position of the shaft center z with eccentricity angle θ and eccentricity ratio ε as shown below,
z= εceIθ
the following approximate equation can be obtained.
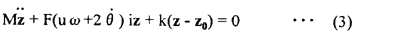
where the angular velocity of the pinion journal is represented by u ω and the second term represents the oil film reaction force as shown below
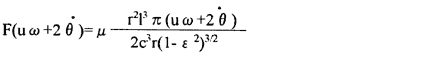
The equivalent mass considering the effect of the moment of inertia should be used as mass M because the angular displacement φ is solely resultant from the displacement x, but the equivalent mass in the direction of x is different from that in y which makes the equations complicated. Approximately, however, it does not give direct influence to the unstable area, therefore, the mass M is used as it is. Moreover, k represents the equivalent spring constant including rigidity of the shaft, gear tooth and oil film and z0 represents the origin of the equivalent spring.
Whence by the assumption of the steady oil whirl, the condition of the approximate unstable criterion can be replaced with condition that the coefficient of the 2nd term of Eq. (3) be positive. As the result, the design criterion taking the direction of the shaft turn opposite is shown as follows.
uω>2ω1 (4)
where it is proposed that the natural circular frequency of the model obtained from the Eq. (2) is used as ω1 in this paper. Eq. (4) does not always stand up for all rpm conditions, but it is applicable to determine the unstable boundary line around the condition of u ω =2ω1 where the natural vibration of the system clearly occurs by the self-exciting vibration.
Fig. 9 shows the calculated results of Eq. (4) superimposed on Fig. 2, where two boundary lines appear each of which corresponds to the natural frequencies of the torsionai vibration of the shafting system and gear tooth rigidity respectively.
It is noted that both lines almost meet the boundary lines obtained by the characteristic equation, i.e., the method of the assumption of the steady oil whirl gives the approximate criterion of unstable boundary line. This give the designer a guide in designing the reduction gear to adopt simple Eq. (4) in the first stage and to use the natural circular frequency of the torsional vibration of the shafting system as ω1.
On the other hand, there exists a line which is located diagonally between both lower and upper lines, which is determined by the energy balance between the damping factor of the shafting and the energy given by the self-exciting vibration. In case of calculating the unstable area with the assumption of damping coefficient as 1/10 of the actual, the diagonal line moves to the left as shown in Fig. 10. Therefore, if the damping is too much to continue steady oil whirl, it is noted that such phenomena as makes the unstable area above the boundary line stable.
5. EXAMPLE OF DIESEL ENGINE PROPULSION SHAFTING
Fig. 11 shows the diesel engine propulsion shafting, which was actually built, consisting of twin engines, a reduction gear and a shaft line. When single engine operation is required, the gear train of idling side is freely driven by the working side engine, which results in the extraordinary vibration on condition that the operating point is in the aforementioned unstable areas.
According to the calculation for this propulsion shafting, the natural frequency is 4.37 Hz and the system becomes unstable above 530rpm. In fact, such phenomena as suddenly excited the extraordinary vibration on the gear casing of the vessel above 570rpm was observed. The measured waveform of the acceleration is shown in Fig. 12.