The following equations (8) and (9) can be obtained by rearranging the expression of equation (6), into which the above-mentioned relational expressions (7) is substituted;
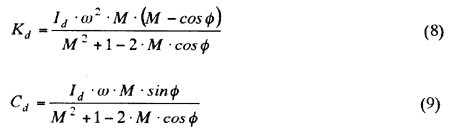
Where M = θdo/θpo. In equations (8) and (9) the values of amplitude ratio M and phase angle θ can be obtained by analyzing harmonically the waveforms measured at the damper inertia ring and the casing. In addition, the values of Id, ω are known. Therefore, the values of dynamic torsional stiffness Kd and damping coefficient Cd can be determined from equations (8) and (9), respectively.
7. EXPERIMENTAL RESULTS AND CONSIDERATIONS
7.1 Experimental Results of Resonant Amplitudes
Table 4 shows the measured natural frequencies and resonant torsional amplitudes obtained from the experiments by the changes of the dimensions of the inertia rings and the viscosities of silicone oil indicated in Table 2 and Table 3, respectively. There are more effective dampers in the reduction of resonant amplitudes than the standard design damper N0.2 which have the optimum clearance 0.5 mm determined from BICERA's experimental equation [27]*, by judging from the results shown in Table 4 on the comparing condition of approximately equal inertia moment of each inertia ring. As some dampers are more effective in resonant amplitude reduction than the standard design damper NO.2, the clearance value given by BICERA's empirical formula [27]* is not always optimum on the every viscosity of the filled silicone oil of the viscous damper.
7.2 Relationship between Resonant Torsional Amplitude and Natural Frequency by Only Change of the Viscosity of Silicone Oil.
Figs. 7 (a) to (c), which are grouped in accordance with approximately equal values of the inertia moments of damper inertia ring, show the relationship between resonant torsional amplitude of the 4.5th order vibration and the natural frequency by the change of the viscosity of silicone oil. Then, the effect of the moment of inertia on the resonant torsional amplitude can be disregarded in each figure. The optimum viscosity which minimizes the resonant amplitude exists in the range of the small clearance, but it does not exist in the range of the large clearance. The effect of resonant amplitude reduction become larger with the increase of the viscosity in large clearance. In addition, the optimum viscosity is different by the clearance dimension between the inside of the casing and the outside of the inertia ring. As mentioned above, the optimum viscosity is different by the dimensions of the peripheral and lateral gaps between the outside of the inertia ring and the inside of the casing.
Fig. 7 (c) Relationship between Resonant Torsional Amplitude and Natural Frequency by Change of Kinematic Viscosity, The Third Part (4.5th Order Vibration, Inertia Rings: No.08, No.09, No.10)
7.3 Relationship between Resonant Torsional Amplitude and Natural Frequency on Conditions of Constant Viscosity of Silicone Oil and Dimensional Change of Clearance
Fig. 8 shows the relationship between the resonant torsional amplitude and the natural frequency obtained by the change of the clearance dimension at every viscosity. The moment of inertia of every inertia ring is approximately equal in Fig. 8. The almost equal tendency at every viscosity is shown in Fig. 8. If the viscosity of the filling silicone oil is originally decided, the optimum clearance in proportion to the viscosity exists.
7.4 Effect of Clearance Dimension on Resonant Torsional Amplitude
Figs.9 (a) and (b) illustrate the relationship between the resonant torsional amplitude and the clearance dimension on conditions of the dimensional changes of (a) the only lateral gap and (b) the only peripheral gap, respectively. As shown in Table 3, the viscosity of the silicone oil is diversely varied in this experiment.