Fig. 6 Amplitude Curves of Torsional Angular Displacement at Damper Inertia Ring (Inertia Ring No. 02)

　

In addition, the damper coefficient K is defined by the following equation (3) [33]^*-[36]^*

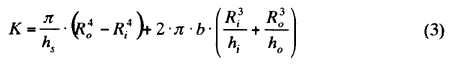
Where, h_s, h_o, h_i: lateral gap, outer-peripheral gap, inner-peripheral gap between damper casing and inertia ring, respectively, R_o, R_i: outer radius, inner radius of damper inertia ring, respectively, b: width of damper inertia ring. The complex coefficient of torsional viscous damping C_d^* is determined from the product of the damper coefficient and equation (2) as follows [28]^*-[32]^*:

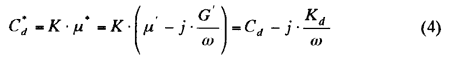
The dynamic characteristics of the complex coefficient of torsional viscous damping are investigated through the examination of torsional damping coefficient C_d and torsional stiffness K_d composed of the real part and the imaginary part of that complex coefficient, respectively: And, the absolute value of the complex coefficient of torsional viscous damping |C_d^*| can be determined by the following equation,

The values of dynamic torsional stiffness and damping coefficient of damper viscous parts can be obtained from the harmonically analyzed results of waveforms measured at the damper inertia ring and the casing. The equation of motion at the damper inertia ring is as follows:

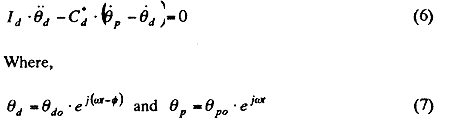
θ_d: torsional angular displacement of damper inertia ring,

θ_p: torsional angular displacement of damper casing.

　

Table 4 Experimental Results of Resonant Torsional Amplitudes

BACK　　　CONTENTS　　　NEXT