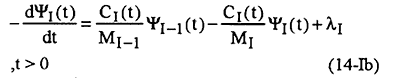
with the final confitions
λi(tf) = 0.0 and ψi(tf) = 0.0, i = 1 to I
The adjoint problems are different from the standard initial value problems in that the final time conditions at time t = tf is specified instead of the customary initial condition. However, this problem can be transformed to an initial value problem by the transformation of the time variables as τ=tf - t. Then the standard techniques of fourth-order Runge-Kutta method can be used to solve the above adjoint problems.

4-3. STOPPING CRITERION
If the problem contains no measurement errors, the traditional check condition is specified as

where ε is a small-specified number. However, the measured displacements may contain measurement errors. Therefore, we do not expect the functional equation (4) to be equal to zero at the final iteration step. Following the experiences of the author [9], we use the discrepancy principle as the stopping criterion, i.e, we assume that the residuals for the displacement and velocity may be approximated by
xi (t)-Xi(t) = σi, i=1 to I (20)
where σi are the standard deviation of the displacement measurements, which are assumed to be a constant. Substituting equation (20) into equation (4), the following expression is obtained for stopping criteria ε:

Then, the stopping criterion is given by equation (19) with ε determined from equation (21).
5. COMPUTATIONAL PROCEDURE
The computational procedure for the solution of this inverse problem using conjugate gradient method may be summarized as follows:

6. RESULTS AND DISCUSSION
The objective of this work is to show the validity of the CGM in estimating simultaneously the external forces fi(t) in the inverse nonlinear force vibration problems with no prior information on the functional form of the unknown quantities.
To illustrate the accuracy of the conjugate gradient method in predicting external forces fi(t) in a damped vibration problem from the knowledge of transient displacement recordings, two specific examples having different form of external forces are considered here.
In order to compare the results for situations involving random measurement errors, we assume normally distributed uncorrelated errors with zero mean and constant standard deviation. The simulated inexact measurement displacement data Xi(t) can be expressed as
Xi(t) = Xi,exact(t) + ω(t)σI (22)
where Xi,exact(t) are the solution of the direct vibration problem with an exact external forces fi(t); σi are the standard deviation of the measured displacements and ωi(t) are the random variables that are generated by subroutine DRNNOR of the IMSL [11] and will be within -2.576 to 2.576 for a 99% confidence bound.

We now present below the nurnerical experiments in determining fi(t) simultaneously by the inverse analysis using the CGM in a two-degree-of-freedom problem, i.e. I = 2.