The solution of the present inverse vibration problem is to be obtained in such a way that the following functional is minimized:

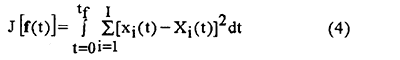
here, x_i(t) are the estimated or computed displacements at time t. These quantities are determined from the solution of the direct problem given previously by using an estimated f_i(t) for the exact f_i(t). Here the hat " ^ " denotes the estimated quantities.

　

4. CONJUGATE GRADIENT METHOD FOR MINIMIZATION

　

The following iterative process based on the conjugate gradient method [9] is now used for the estimation of time dependent external forces f_i(t) by minimizing the functional J[f(t)]

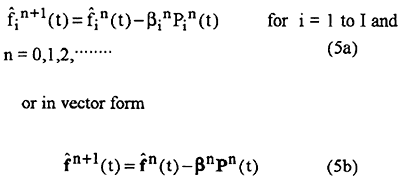
where β_iⁿ are the search step sizes going from n iteration n to iteration n+1, and P_iⁿ(t) are the directions of descent (i.e. search directions) given by

P_iⁿ=J_i'ⁿ(t) + γ_iⁿP_i^N-1 (6a)

or in vector form

Pⁿ⁺¹=J'ⁿ(t) - γⁿP^n-1(t) (6b)

which are a conjugation of the gradient directions J_i'ⁿ(t) at iteration n and the directions of descent

P_i^n-1(t) at iteration n-1. The conjugate coefficients are determined from

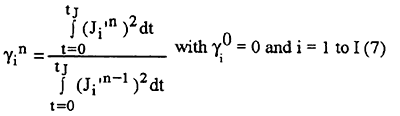
We note that when γ_iⁿ=0 for any n, in equation (7), the directions of descent P_iⁿ(t) become the gradient direction, i.e. the "Steepest descent" method is obtained. The convergence of the above iterative procedure in minimizing the functional J is guaranteed in the paper by Lasdon et al. [10].

To perform the iteration s according to equation (5), we need to compute the step sizes β_iⁿ and the gradient of the functional J'_iⁿ(t). In order to develop expressions for the determination of these two quantities, a "sensitivity problem" and an "adjoint problem" are constructed as described below.

　

4-1. SENSITIVITY PROBLEM AND SEARCH STEP SIZE

　

Since the problem involves I unknown time-dependent external forces f = f_i(t_n) = {f₁(t_n),…, f₁(t _n)} , n = 1 to N. In order to derive the sensitivity problem for each unknown function, we should perturb one unknown external force at a time.

It is assumed that when f_i(t) undergoes a variation Δf_i(t)gδ(i-j), whereδ(・) is the Dirac-delta function and j = 1 to I, X_i(t) and y_i(t) are perturbed by Δx_i,j(t) and Δy_i,j(t). Then replacing in the direct problem f_i(t) by f_i(t)+Δf_i(t)δ_(i-j), x_i(t) by x_i(t)+ Δx_ij(t) and y_i(t) by y_i(t)+ Δy_i,j(t), subtracting from the resulting expressions the direct problem and neglecting the second-order terms, we obtained the following I sensitivity problems, (i,e, j = 1 to I), for the sensitivity functions Δx_i,j(t) and Δy_i,j(t).

　

　

　

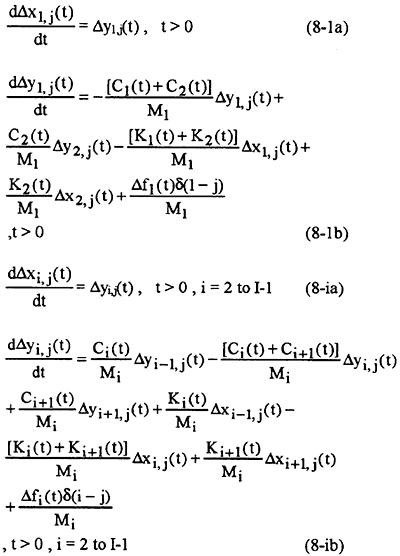
BACK　　　CONTENTS　　　NEXT