Finally the inverse solutions for a damped vibration problem with different types of external forces will be illustrated to show the validity of using the CGM in the present inverse vibration problem.
2. THE DIRECT PROBLEM
To illustrate the methodology for developing expressions for use in determining the unknown time-dependent external forces simultaneously in a nonlinear multiple-degree-of-freedom vibration problem, (i.e. the damping coefficient Ci(t) and stiffness coefficients Ki(t) are both function of time), we consider the following damped force vibration problem.
The initial conditions of displacement and velocity for the multiple-degree-of-freedom system
where subscript i=1 to I, and I represents I-degree-of-freedom. When t > 0, the system parameters Ki(t) and Ci(t) are given, moreover the time-dependent external forces f=fi(tn)={f1(tn),…, f1l(tn)}, n = 1 to N and N represents the total discretized number of time, are also assumed known.
The system under consideration here is shown in Figure 1 and the mathematical formulation of this multiple-degree-of-freedom problem is given by:
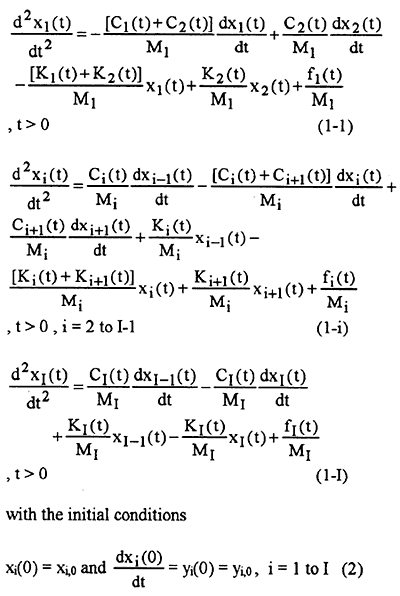
Here Mi represents the mass of the subsystem. There exists no exact solution for equation (1) for any arbitrary function of Ki(t). Ci(t) and fi(t). For this reason the numerical solution with the technique of the fourth-order Runge-Kutta method will be applied to solve equation (1) by reducing it into (2 X I) coupled first-order ordinary differential equations as shown below:
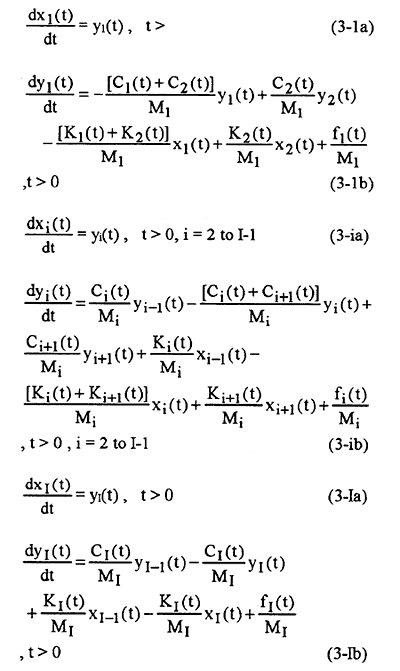
The direct problem considered here is concerned with the determination of the system displacement xi(t) and velocity yi(t) when the initial conditions, the system parameters, Ki(t) and Ci(t), and the time-dependent external forces fi(t) are all given.
Here the fourth-order Runge-Kutta method is used to solve the system of equation (3).
3. THE INVERSE PROBLEM
For the inverse problem, the time-dependent external forces fi(t) are regarded as being unknown, but everything else in equations (3) are known. In addition, system displacements measured at some appropriate time are considered available.
Let the measured system displacements with time be denoted by Xi(t), here t = 0 to tf, and tf represents the final time of the measurements. Then the inverse problem can be stated as follows: by utilizing the above mentioned measured system displacements data, Xi(t), to estimate simultaneously the unknown time-dependent external forces fi(t).
In the present study, we haven't used real measured system displacements, rather, we used the assigned exact external forces to generate the simulated values of Xi(t), then try to retrieve the time-dependent external forces fi(t) by using Xi(t) and initial guesses of external forces.