10Ca(HCO3)2+6Na3P04+2NaOH→
[Ca3(PO4)2]3・ Ca(OH)2+10Na2CO3+10CO2+10H20 (1)
10CaCl2+6Na3PO4+2NaOH→
[Ca3(PO4)2]3・Ca(OH)2+20NaCl (2)
Mg(HCO3)2+SiO2+2NaOH→
MgSiO3+Na2CO3+CO2+2H2O (3)
Mg(HCO3)2+2NaOH→Mg(OH)2+Na2CO3+CO2+H2O (4)
MgCl2+SiO2+2NaOH→MgSiO3+2NaCl+H2O (5)
MgCl2+2NaOH→Mg(OH)2+2NaCl (6)
SiO2+2NaOH→Na2SiO3+H2O (7)
Focusing on ion reactions in eqs.(1) to (7), and disregarding SiO2 effect due to its little concentration in seawater, the simple resultant reactions can be derived as the ion reactions of eqs. (8) and (9) . The pH, EC and PO43- concentration can be derived by the use of these.
10Ca2++6PO43-+2OH-→[Ca3(PO4)2]3・Ca(OH)2 (8)
Mg2++2OH-→Mg(OH)2 (9)
2.2 New chemical reaction system proposed here
According to the results of our third paper, a new chemical reaction system can be introduced as shown in eqs.(10) to (13) instead of eqs. (3) to (6). A point of the difference is to reconsider the effect of Mg.
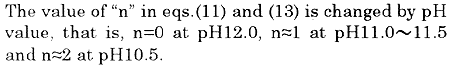
Mg(HCO3)2+SiO2+2NaOH→
MgSiO3+Na2CO3+CO2+2H2O (10)
(3n+1)Mg(HCO3)2+2nNa3PO4+2NaOH→
[Mg3(PO4)2]n・Mg(OH)2 + (3n+1)Na2CO3 + (3n+1)CO2 + (3n+1)H2O (11)
MgCl2+SiO2+2NaOH→MgSiO3+2NaCl+H2O (12)
(3n+1)MgCl2+2nNa3PO4+2NaOH→
[Mg3(PO4)2]n・Mg(OH)2 + (6n+2) NaCl (13)
When there is little SiO2, eqs.(1), (2), (11), (13) are a system of the new chemical reaction model in the case when seawater mixed into boiler water. In the case when SiO2 coexists with Mg and Ca in the feed water, eqs.(1), (2), (10), (12) are the another system of the new chemical reaction model. The simple resultant reactions can be derived as ion reactions from the new models. Eqs.(14), (15)and (16) are consequently derived. Those are eqs.(14) and (15) for the former case little SiO2, and eqs.(14) and (16) for the latter case of SiO2 coexistence.
10Ca2++6PO43-+2OH-→[Ca3(PO4)2]3Ca(OH)2 (14)
(3n+1)Mg2++2nPO43-+2OH-→ [Mg3(PO4)2]n・Mg(OH)2 (15)
Mg2++SiO2+2OH-→MgSiO3+H2O (16)
3. WATER QUALITY ESTIMATION BASED ON THE NEW CHEMICAL REACTION MODEL
In order to confirm the validity of new proposed model, the change of boiler water quality due to seawater mixing is estimated by the new model and is compared with the experimental results in chapter 3 and 4.
3.1 Theoretical estimation by seawater mixing
Using the ion reactions of eqs.(14) and (15), it is possible to estimate the change of water quality when sea water is mixed. In order to carry out this estimation, it is necessary at first to calculate the P-alkalinity consumption in chemical reaction eqs. (1), (2), (11), (18). Because, the effect of the M-alkalinity components is neglected in the ion reactions.
3.1.1 Consumption of P-alkalinity
Table 1 shows components of the seawater used in the second paper. Since it can be read out from Table 1 that there exists a relation of "Total hardness > Carbonate hardness > Zero", P-alkalinity consumption due to hardness components can be calculated as the following procedure . In the following, then n=1 is adopted in eq. (15), because the experiment is carried out in 11.0 to 11.5 of pH.
From eq. (1), PA1=(1+α) *Ca1/2-0.4 *Ca1,
from eq. (2), PA2=-0.4*Ca2,
from eq. (11), PA11=(1+α)*Mg1/2-0.5*Mg1,
from eq. (13), PA13=-0.5*Mg2,
PAc=PA1+PA2+PA11+PA13,
=(1+α)*(Ca1+Mg1)/2-0.4*(Ca1+Ca2)-0.5*(Mg1+Mg2)
=(1+α)*MA/2-0.5*H+0.1*CaH
=(1+0.625)*105/2-0.5*(358*100/40.08+1260*100/24.305)+0.1* (358*100/40.08)
=-2864 (mgCaCO3/1),
where, PAc ; P-alkalinity consumption estimated from the chemical equations, PA1,PA2, PA10,PA11,PA12,PA13; P-alkalinity estimated from each corresponding eq., respectively, Ca1; carbonate calcium hardness, Ca2 ; non-carbonate calcium hardness, Mg1; carbonate magnesium hardness, Mg2; non-carbonate magnesium hardness, CaH; calcium hardness, H; total hardness, MA; carbonate hardness, H-MA; non-carbonate hardness, α; decomposition rate of sodium carbonate Na2CO3 (α≒0.625 when the boiler pressure is 1.6 MPa according to Kurita[4].)
Further, those above e quations give the following relations.
CaH=Ca1+Ca2=358mg/l,
H=Ca1+Ca2+Mg1+Mg2=358mg/l+1260mg/l,
MA=Ca1+Mg1=105mg/l
P alkalinity consumed in eqs. (14) and (15) can be calculated as the follows.
From eg. (14), PA14=-0.1*CaH,
from eg. (15), PA15=-0.25*MgH,
PAI= PA14+PA15=-0.1*358*100/40.08-0.25*1260*100/24.305=-1384(mgCaCO3/l)
where, PAI; P alkalinity estimated from the ion equations, CaH (mgCaCO3/l); calcium hardness, MgH (mgCaCO3/l); magnesium hardness.